
 如图,点D是△ABC的边AB的延长线上一点,点F是边BC上的一个动点(不与点B重合).以BD、BF为邻边作平行四边形BDEF,又AP$\underset{∥}{=}$BE(点P、E在直线AB的同侧),如果BD=$\frac{1}{3}$AB,那么△PBC的面积与△ABC面积之比为2:3.
如图,点D是△ABC的边AB的延长线上一点,点F是边BC上的一个动点(不与点B重合).以BD、BF为邻边作平行四边形BDEF,又AP$\underset{∥}{=}$BE(点P、E在直线AB的同侧),如果BD=$\frac{1}{3}$AB,那么△PBC的面积与△ABC面积之比为2:3. 分析 首先过点P作PH∥BC交AB于H,连接CH,PE,易得四边形APEB,BFPH是平行四边形,又由四边形BDEF是平行四边形,设BD=a,则AB=3a,可求得BH=PF=2a,又由S△HBC=S△PBC,S△HBC:S△ABC=BH:AB,即可求得△PBC的面积与△ABC面积之比.
解答 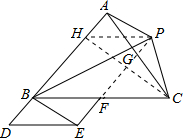 解:过点P作PH∥BC交AB于H,连接CH,PE,
解:过点P作PH∥BC交AB于H,连接CH,PE,
∵AP$\underset{∥}{=}$BE,
∴四边形APEB是平行四边形,
∴PE∥AB,PE=AB,
∵四边形BDEF是平行四边形,
∴EF∥BD,EF=BD,
即EF∥AB,
∴P,E,F共线,
设BD=a,
∵BD=$\frac{1}{3}$AB,
∴PE=AB=3a,
则PF=PE-EF=2a,
∵PH∥BC,
∴S△HBC=S△PBC,
∵PF∥AB,
∴四边形BFPH是平行四边形,
∴BH=PF=2a,
∵S△HBC:S△ABC=BH:AB=2a:3a=2:3,
∴S△PBC:S△ABC=2:3.
故答案为:2:3.
点评 此题考查了平行四边形的判定与性质与三角形面积比的求解方法.此题难度较大,注意准确作出辅助线,掌握等高三角形面积的比等于其对应底的比是关键.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
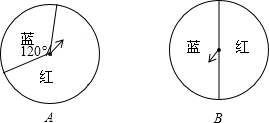 游戏者同时转动如图的两个转盘进行“配紫色游戏”,若要使游戏者获胜的概率为$\frac{1}{10}$,转盘B不动,转盘A应该如何设计?并写出解答过程说明理由.
游戏者同时转动如图的两个转盘进行“配紫色游戏”,若要使游戏者获胜的概率为$\frac{1}{10}$,转盘B不动,转盘A应该如何设计?并写出解答过程说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 评委代号 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ |
| 评分(单位:分) | 85 | 90 | 80 | 95 | 90 | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com