
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的⊙O与AD,AC分别交于点E,F,且∠ACB=∠DCE.
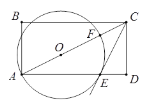
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=![]() ,BC=4,求⊙O的半径.
,BC=4,求⊙O的半径.
【答案】(1)直线CE与⊙O相切,理由详见解析;(2)![]()
【解析】
(1)连接OE,由四边形ABCD是矩形,得到∠3=∠1,∠2+∠5=90°,而OA=OE,∠1=∠2,所以∠3=∠4,∠4=∠2,故∠4+∠5=90°得到∠OEC=90°,根据切线的判定定理即得到CE是⊙O的切线;
(2)作OG⊥AE交线段AE于G点,根据tan∠ACB=![]() 先求出AB的长度和DE的长度,然后分别求出AG和OG的长度,利用勾股定理求出OA的长度即可解答.
先求出AB的长度和DE的长度,然后分别求出AG和OG的长度,利用勾股定理求出OA的长度即可解答.
(1)直线CE与⊙O相切.
证明:如图,连接OE,

∵ 矩形ABCD中,BC∥AD, ∴ ∠1=∠3.
又∠1=∠2, ∴ ∠2=∠3.
则∠3=∠4.
∴ ∠2=∠4.
∵ ∠2+∠5=90°, ∴ ∠4+∠5=90°.
∴ ∠OEC=90°,即OE⊥CE, ∴ 直线CE与⊙O相切.
(2)解:∵ tan ∠ACB=![]() =
=![]() , BC=4.
, BC=4.
∴ AB=BC·tan ∠ACB=2.
又 ∠1=∠2.
∴ DE=DC·tan ∠DCE= DC·tan ∠ACB= 1.
过点O作OG⊥AE于点G,则 AG=![]() AE=
AE=![]() .
.
∵ OG=AG·tan∠DAC= AG·tan∠ACB =![]() ×
×![]() =
=![]() ,
,
∴ OA=![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
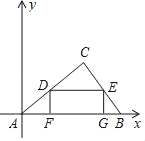
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,以点A为原点建立平面直角坐标系,使AB在x轴正半轴上,点D是AC边上的一个动点,DE∥AB交BC于E,DF⊥AB于F,EG⊥AB于G.以下结论:
①△AFD∽△DCE∽△EGB;
②当D为AC的中点时,△AFD≌△DCE;
③点C的坐标为(3.2,2.4);
④将△ABC沿AC所在的直线翻折到原来的平面,点B的对应点B1的坐标为(1.6,4.8);
⑤矩形DEGF的最大面积为3.在这些结论中正确的有_____(只填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为奖励在艺术节系列活动中表现优秀的同学,计划购买甲、乙两种奖品.已知购买甲种奖品30件和乙种奖品25件需花费1950元,购买甲种奖品15件和乙种奖品35件需花费1650元.
(1)求甲、乙两种奖品的单价;
(2)学校计划购买甲、乙两种奖品共1800件,其中购买乙种奖品的件数不超过甲种奖品件数的2倍,学校分别购买甲、乙两种奖品多少件才能使总费用最小?最小费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
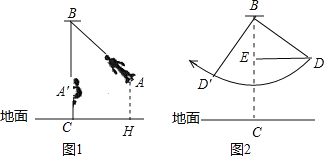
【题目】如图1,是小明荡秋千的侧面示意图,秋千链长AB=5m(秋千踏板视作一个点),静止时秋千位于铅垂线BC上,此时秋千踏板A到地面的距离为0.5m.
(1)当摆角为37°时,求秋千踏板A与地面的距离AH;(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
(2)如图2,当秋千踏板摆动到点D时,点D到BC的距离DE=4m;当他从D处摆动到D'处时,恰好D'B⊥DB,求点D'到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
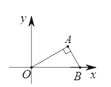
【题目】将直角三角形纸板OAB按如图所示方式放置在平面直角坐标系中,OB在x轴上,OB=4,OA=2![]() 将三角形纸板绕原点O逆时针旋转,每秒旋转60°,则第2019秒时,点A的对应点A ′ 的坐标为( )
将三角形纸板绕原点O逆时针旋转,每秒旋转60°,则第2019秒时,点A的对应点A ′ 的坐标为( )
A. (-3,-![]() )B. (3,-
)B. (3,-![]() )C. (-3,
)C. (-3,![]() )D. (0,2
)D. (0,2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,AB⊥BC于点B,AD=4,将CD绕点D逆时针旋转90°至DE,连接AE、CE,若△ADE的面积为6,则BC=_____.
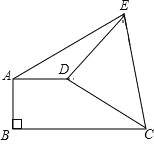
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一种动画设计,屏幕上的长方形ABCD是黑色区域(含长方形的边界),其中A(﹣1,1)、B(2,1)、C(2,2),D(﹣1,2),用信号枪沿直线y=kx﹣2发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的k的取值范围是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长BC=8cm,宽AB=4cm的矩形纸片ABCD折叠,使点C与点A重合,则折痕EF的长为( )

![]()

A. 4cmB. ![]() cmC.
cmC. ![]() cmD.
cmD. ![]() cm
cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com