
【题目】将直角三角形纸板OAB按如图所示方式放置在平面直角坐标系中,OB在x轴上,OB=4,OA=2![]() 将三角形纸板绕原点O逆时针旋转,每秒旋转60°,则第2019秒时,点A的对应点A ′ 的坐标为( )
将三角形纸板绕原点O逆时针旋转,每秒旋转60°,则第2019秒时,点A的对应点A ′ 的坐标为( )
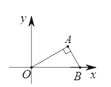
A. (-3,-![]() )B. (3,-
)B. (3,-![]() )C. (-3,
)C. (-3,![]() )D. (0,2
)D. (0,2![]() )
)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】郑州市创建国家生态园林城市实施方案已经出台,到2019年5月底,市区主城区要达到或超过《国家生态园林城市标准》各项指标要求.郑州市林荫路推广率要超过85%,在推进此活动中,郑州市某小区决定购买A、B两种乔木树,经过调查,获取信息如下:如果购买A种树木40棵,B种树木60棵,需付款11400元;如果购买A种树木50棵,B种树木50棵,需付款10500元.
树种 | 购买数量低于50棵 | 购买数量不低于50棵 |
A | 原价销售 | 以八折销售 |
B | 原价销售 | 以九折销售 |
(1)A种树木与B种树木的单价各多少元?
(2)经过测算,需要购置A、B两种树木共100棵,其中B种树木的数量不多于A种树木的三分之一,如何购买付款最少?最少费用是多少元?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高_____________米(结果保留根号).
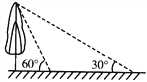
查看答案和解析>>
科目:初中数学 来源: 题型:
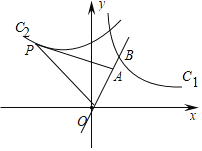
【题目】如图,将曲线c1:y=![]() (x>0)绕原点O逆时针旋转60°得到曲线c2,A为直线y=
(x>0)绕原点O逆时针旋转60°得到曲线c2,A为直线y=![]() x上一点,P为曲线c2上一点,PA=PO,且△PAO的面积为6
x上一点,P为曲线c2上一点,PA=PO,且△PAO的面积为6![]() ,直线y=
,直线y=![]() x交曲线c1于点B,则OB的长( )
x交曲线c1于点B,则OB的长( )
A.2![]() B.5C.3
B.5C.3![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
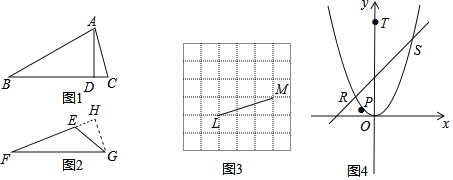
【题目】如果一个三角形有一条边上的高等于这条边的一半,那么我们把这个三角形叫做“半高三角形”.
如图1,对于△ABC,BC边上的高AD等于BC的一半,△ABC就是半高三角形,此时,称△ABC是BC类半高三角形;如图2,对于△EFG,EF边上的高GH等于EF的一半,△EFG就是半高三角形,此时,称△EFG是EF类半高三角形.
(1)直接写出下列3个小题的答案.
①若一个三角形既是等腰三角形又是半高三角形,则其底角度数的所有可能值为 .
②若一个三角形既是直角三角形又是半高三角形,则其最小角的正切值为 .
③如图3,正方形网格中,L,M是已知的两个格点,若格点N使得△LMN为半高三角形,且△LMN为等腰三角形或直角三角形,则这样的格点N共有 个.
(2)如图,平面直角坐标系内,直线y=x+2与抛物线y=x2交于R,S两点,点T坐标为(0,5),点P是抛物线y=x2上的一个动点,点Q是坐标系内一点,且使得△RSQ为RS类半高三角形.
①当点P介于点R与点S之间(包括点R,S),且PQ取得最小值时,求点P的坐标.
②当点P介于点R与点O之间(包括点R,O)时,求PQ+![]() QT的最小值.
QT的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的⊙O与AD,AC分别交于点E,F,且∠ACB=∠DCE.
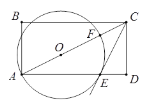
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=![]() ,BC=4,求⊙O的半径.
,BC=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需要的时间与原计划生产450台机器所需要的时间相同.
(1)原计划平均每天生产多少台机器?
(2)若该工厂要在不超过5天的时间,生产1100台机器,则平均每天至少还要再多生产多少台机器?
查看答案和解析>>
科目:初中数学 来源: 题型:
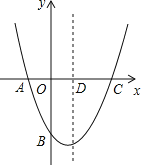
【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx-![]() 的图象经过点A(-1,0)、C(2,0),与y轴交于点B,其对称轴与x轴交于点D
的图象经过点A(-1,0)、C(2,0),与y轴交于点B,其对称轴与x轴交于点D
(1)求二次函数的表达式及其顶点坐标;
(2)M(s,t)为抛物线对称轴上的一个动点,
①若平面内存在点N,使得A、B、M、N为顶点的四边形为矩形,直接写出点M的坐标;
②连接MA、MB,若∠AMB不小于60°,求t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com