
ЁОЬтФПЁПШчЙћвЛИіШ§НЧаЮгавЛЬѕБпЩЯЕФИпЕШгкетЬѕБпЕФвЛАыЃЌФЧУДЮвУЧАбетИіШ§НЧаЮНазіЁААыИпШ§НЧаЮЁБЃЎ
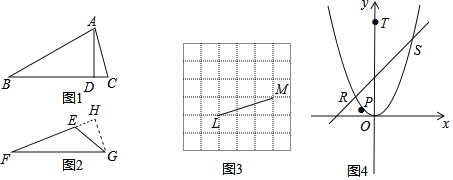
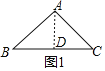
ШчЭМ1ЃЌЖдгкЁїABCЃЌBCБпЩЯЕФИпADЕШгкBCЕФвЛАыЃЌЁїABCОЭЪЧАыИпШ§НЧаЮЃЌДЫЪБЃЌГЦЁїABCЪЧBCРрАыИпШ§НЧаЮЃЛШчЭМ2ЃЌЖдгкЁїEFGЃЌEFБпЩЯЕФИпGHЕШгкEFЕФвЛАыЃЌЁїEFGОЭЪЧАыИпШ§НЧаЮЃЌДЫЪБЃЌГЦЁїEFGЪЧEFРрАыИпШ§НЧаЮЃЎ
ЃЈ1ЃЉжБНгаДГіЯТСа3ИіаЁЬтЕФД№АИЃЎ
ЂйШєвЛИіШ§НЧаЮМШЪЧЕШбќШ§НЧаЮгжЪЧАыИпШ§НЧаЮЃЌдђЦфЕзНЧЖШЪ§ЕФЫљгаПЩФмжЕЮЊЁЁ ЃЎ
ЂкШєвЛИіШ§НЧаЮМШЪЧжБНЧШ§НЧаЮгжЪЧАыИпШ§НЧаЮЃЌдђЦфзюаЁНЧЕФе§ЧажЕЮЊЁЁ ЃЎ
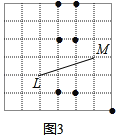
ЂлШчЭМ3ЃЌе§ЗНаЮЭјИёжаЃЌLЃЌMЪЧвбжЊЕФСНИіИёЕуЃЌШєИёЕуNЪЙЕУЁїLMNЮЊАыИпШ§НЧаЮЃЌЧвЁїLMNЮЊЕШбќШ§НЧаЮЛђжБНЧШ§НЧаЮЃЌдђетбљЕФИёЕуNЙВгаЁЁ ИіЃЎ
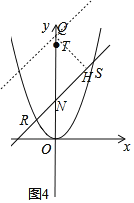
ЃЈ2ЃЉШчЭМЃЌЦНУцжБНЧзјБъЯЕФкЃЌжБЯпyЃНx+2гыХзЮяЯпyЃНx2НЛгкRЃЌSСНЕуЃЌЕуTзјБъЮЊЃЈ0ЃЌ5ЃЉЃЌЕуPЪЧХзЮяЯпyЃНx2ЩЯЕФвЛИіЖЏЕуЃЌЕуQЪЧзјБъЯЕФквЛЕуЃЌЧвЪЙЕУЁїRSQЮЊRSРрАыИпШ§НЧаЮЃЎ
ЂйЕБЕуPНщгкЕуRгыЕуSжЎМфЃЈАќРЈЕуRЃЌSЃЉЃЌЧвPQШЁЕУзюаЁжЕЪБЃЌЧѓЕуPЕФзјБъЃЎ
ЂкЕБЕуPНщгкЕуRгыЕуOжЎМфЃЈАќРЈЕуRЃЌOЃЉЪБЃЌЧѓPQ+![]() QTЕФзюаЁжЕЃЎ
QTЕФзюаЁжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй45ЁуЁЂ15ЁуЁЂ75ЁуЃЛЂк1Лђ![]() ЃЛЂл7ЃЛ ЃЈ2ЃЉЂйЕуPЁфЃЈ
ЃЛЂл7ЃЛ ЃЈ2ЃЉЂйЕуPЁфЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌДЫЪБЃЌPЃЈPЁфЃЉQШЁЕУзюаЁжЕЃЛЂкЕБЕуPгыЕуRжиКЯЃЌЧвPЁЂQЁЂHдквЛЬѕжБЯпЧвгыжБЯпHTДЙжБЪБЃЌPQ+
ЃЉЃЌДЫЪБЃЌPЃЈPЁфЃЉQШЁЕУзюаЁжЕЃЛЂкЕБЕуPгыЕуRжиКЯЃЌЧвPЁЂQЁЂHдквЛЬѕжБЯпЧвгыжБЯпHTДЙжБЪБЃЌPQ+![]() QTгазюаЁжЕЃЌзюаЁжЕЮЊ4ЃЎ
QTгазюаЁжЕЃЌзюаЁжЕЮЊ4ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЂйЂкЗжЕзБпЩЯЕФИпЕШгкЕзБпЕФвЛАыЁЂбќЩЯЕФИпЕШгкбќГЄЕФвЛАыСНжжЧщПіЗжБ№ЧѓНтМДПЩЃЛЂлШчЭМ3ЃЌетбљЕФИёЕуNЙВга7ИіЃЛ
ЃЈ2ЃЉЂйШчЭМ4ЃЌЕБЕуPНщгкЕуRгыЕуSжЎМфЪБЃЌгыRSЦНааЧвгыХзЮяЯпжЛгавЛИіНЛЕуPЁфЪБЃЌPQШЁЕУзюаЁжЕЃЌМДПЩЧѓНтЃЛЂкЕБЕуPгыЕуRжиКЯЃЌЧвPЁЂQЁЂHдквЛЬѕжБЯпЧвгыжБЯпHTДЙжБЪБЃЌPQ+![]() QTгазюаЁжЕЃЌМДПЩЧѓНтЃЎ
QTгазюаЁжЕЃЌМДПЩЧѓНтЃЎ
ЃЈ1ЃЉЂйЕБЕзБпЩЯЕФИпЕШгкЕзБпЕФвЛАыЪБЃЌ
ШчЯТЭМЁїABCЮЊЕШбќШ§НЧаЮЃЌABЃНACЃЌADЃН![]() BCЃЌ
BCЃЌ
дђADЃНCDЃЌдђЁЯBЃНЁЯCЃН45ЁуЃЛ
ЕБбќЩЯЕФИпЕШгкбќГЄЕФвЛАыЪБЃЌ
ЭЌРэЕзНЧЮЊ75ЁуЛђ15ЁуЃЌ
ЙЪЃКД№АИЮЊ45ЁуЁЂ15ЁуЁЂ75ЁуЃЛ
ЂкЕБЕзБпЩЯЕФИпЕШгкЕзБпЕФвЛАыЪБЃЌШчЩЯЭМЃЌЁїABCЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ЙЪзюаЁНЧЮЊ45ЁуЃЌзюаЁНЧЕФе§ЧажЕЮЊ1ЃЛ
бќЩЯЕФИпЕШгкбќГЄЕФвЛАыЪБЃЌЭЌРэПЩЕУЃКзюаЁНЧЕФе§ЧажЕЮЊ![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊ1Лђ![]() ЃЛ
ЃЛ
ЂлШчЭМ3ЃЌетбљЕФИёЕуNЙВга7ИіЃЌОпЬхЧщПіМћЯТЭМЃЌаЁКкЕуЫљЪОЕФЮЛжУЃЌ
ЃЈ2ЃЉНЋХзЮяЯпгыжБЯпЗНГЬСЊСЂВЂНтЕУЃКxЃНЉ1Лђ2ЃЌ
МДЃКЕуRЁЂSЕФзјБъЗжБ№ЮЊЃЈЉ1ЃЌ1ЃЉЁЂЃЈ2ЃЌ4ЃЉЃЌдђRSЃН![]() ЃЌ
ЃЌ
дђRSБпЩЯЕФИпЮЊ![]() ЃЌ
ЃЌ
дђЕуQдкгкRSЦНааЕФЩЯЯТСНЬѕжБЯпЩЯЃЌШчЯТЭМЃЌ
Й§ЕуQзїQHЁЭNHНЛгкЕуHЃЌдђHQЃН![]() ЃЌдђQNЃН
ЃЌдђQNЃН![]() ЃН3ЃЌ
ЃН3ЃЌ
ЕуNЃЈ0ЃЌ2ЃЉЃЌдђЕуMЃЈ5ЃЌ0ЃЉЃЌЕуMгкЕуTжиКЯЃЌ
дђЕуQЕФжБЯпЗНГЬЮЊЃКyЃНx+5ЃЌ
ЕБИУжБЯпдкжБЯпRSЕФЯТЗНЪБЃЌyЃНxЉ1ЃЌ
ЙЪЕуQЫљдкЕФжБЯпЗНГЬЮЊЃКyЃНx+5ЛђyЃНxЉ1ЃЛ
ЂйШчЭМ4ЃЌЕБЕуPНщгкЕуRгыЕуSжЎМфЪБЃЌ
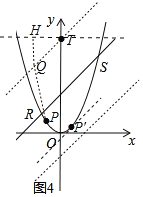
ЩшгыRSЦНааЧвгыХзЮяЯпжЛгавЛИіНЛЕуPЁфЕФжБЯпЗНГЬЮЊЃКyЃНx+dЃЌ
НЋИУЗНГЬгкХзЮяЯпЗНГЬСЊСЂВЂећРэЕУЃКx2ЉxЉdЃН0ЃЌ
ЁїЃН1+4dЃН0ЃЌНтЕУЃКdЃНЉ![]() ЃЌ
ЃЌ
ДЫЪБЃЌx2Љx+![]() ЃН0ЃЌНтЕУЃКxЃН
ЃН0ЃЌНтЕУЃКxЃН![]() ЃЌ
ЃЌ
ЕуPЁфЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌДЫЪБЃЌPЃЈPЁфЃЉQШЁЕУзюаЁжЕЃЛ
ЃЉЃЌДЫЪБЃЌPЃЈPЁфЃЉQШЁЕУзюаЁжЕЃЛ
ЂкЕБЕуPНщгкЕуRгыЕуOжЎМфЃЈАќРЈЕуRЃЌOЃЉЪБЃЌ
ШчЭМ4ЃЌСЌНгPQЃЌЙ§ЕуQзїQHДЙжБЙ§ЕуTгкxжсЦНааЕФжБЯпгкЕуHЃЌ
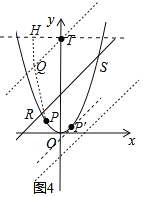
дђHQЃН![]() QTЃЌ
QTЃЌ
PQ+![]() QTЃНPQ+QHЃЌ
QTЃНPQ+QHЃЌ
ЕБЕуPгыЕуRжиКЯЃЌЧвPЁЂQЁЂHдквЛЬѕжБЯпЧвгыжБЯпHTДЙжБЪБЃЌPQ+![]() QTгазюаЁжЕЃЌ
QTгазюаЁжЕЃЌ
дђЦфзюаЁжЕЮЊyTЉyRЃН5Љ1ЃН4ЃЎ


 гЂгяаЁгЂалЬьЬьФЌаДЯЕСаД№АИ
гЂгяаЁгЂалЬьЬьФЌаДЯЕСаД№АИ ЪюМйзївЕАВЛеЩйФъЖљЭЏГіАцЩчЯЕСаД№АИ
ЪюМйзївЕАВЛеЩйФъЖљЭЏГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
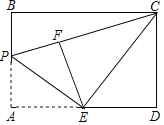
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌABЃН4ЃЌADЃН6ЃЌЕуEЮЊADЕФжаЕуЃЌЕуPЮЊЯпЖЮABЩЯвЛИіЖЏЕуЃЌСЌНгEPЃЌНЋЁїAPEбиEPелЕўЕУЕНЁїEPFЃЌСЌНгCEЃЌCFЃЌЕБЁїECFЮЊжБНЧШ§НЧаЮЪБЃЌAPЕФГЄЮЊ______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
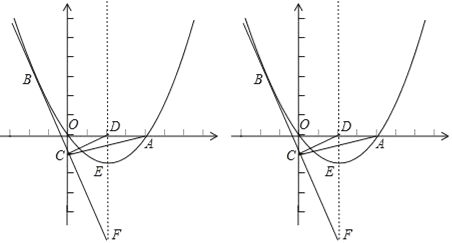
ЁОЬтФПЁПШчЭМЃЌвбжЊвбжЊХзЮяЯпОЙ§дЕуOКЭxжсЩЯвЛЕуAЃЈ4ЃЌ0ЃЉЃЌХзЮяЯпЖЅЕуЮЊEЃЌЫќЕФЖдГЦжсгыxжсНЛгкЕуDЃЌжБЯпy=Љ2xЉ1ОЙ§ХзЮяЯпЩЯвЛЕуBЃЈЉ2ЃЌmЃЉЧвгыyжсНЛгкЕуCЃЌгыХзЮяЯпЕФЖдГЦжсНЛгкЕуFЃЎ
ЃЈ1ЃЉЧѓmЕФжЕМАИУХзЮяЯпЕФНтЮіЪН
ЃЈ2ЃЉPЃЈxЃЌyЃЉЪЧХзЮяЯпЩЯЕФвЛЕуЃЌШєSЁїADP=SЁїADCЃЌЧѓГіЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЃЎ
ЃЈ3ЃЉЕуQЪЧЦНУцФкШЮвтвЛЕуЃЌЕуMДгЕуFГіЗЂЃЌбиЖдГЦжсЯђЩЯвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШдШЫйдЫЖЏЃЌЩшЕуMЕФдЫЖЏЪБМфЮЊtУыЃЌЪЧЗёФмЪЙвдQЁЂAЁЂEЁЂMЫФЕуЮЊЖЅЕуЕФЫФБпаЮЪЧСтаЮЃПШєФмЃЌЧыжБНгаДГіЕуMЕФдЫЖЏЪБМфtЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫНтЮвЪаОХФъМЖбЇЩњЩэЬхЫижЪЧщПіЃЌДгШЋЪаОХФъМЖбЇЩњжаЫцЛњГщШЁСЫВПЗжбЇЩњНјааСЫвЛДЮЬхг§ПМЪдПЦФПВтЪдЃЈАбВтЪдНсЙћЗжЮЊЫФИіЕШМЖЃКAМЖЃКгХауЃЛBМЖЃКСМКУЃЛCМЖЃКМАИёЃЛDМЖЃКВЛМАИёЃЉЃЌВЂНЋВтЪдНсЙћЛцГЩСЫШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЎЧыИљОнЭГМЦЭМжаЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
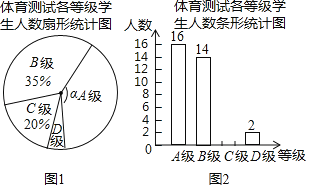
ЃЈ1ЃЉБОДЮГщбљВтЪдЕФбЇЩњШЫЪ§ЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉЭМ1жаЁЯІСЕФЖШЪ§ЪЧЁЁ ЁЁЁуЃЌАбЭМ2ЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉШЋЪаОХФъМЖгабЇЩњ6200УћЃЌШчЙћШЋВПВЮМгетДЮЬхг§ПЦФПВтЪдЃЌЧыЙРМЦВЛМАИёЕФШЫЪ§ЮЊЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
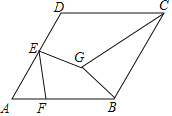
ЁОЬтФПЁПШчЭМЃЌСтаЮABCDЕФБпГЄЮЊ4ЃЌЁЯAЃН60ЁуЃЌEЪЧБпADЕФжаЕуЃЌFЪЧБпBCЩЯЕФвЛИіЖЏЕуЃЌEGЃНEFЃЌЧвЁЯGEFЃН60ЁуЃЌдђGB+GCЕФзюаЁжЕЮЊ__ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
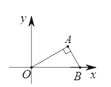
ЁОЬтФПЁПНЋжБНЧШ§НЧаЮжНАхOABАДШчЭМЫљЪОЗНЪНЗХжУдкЦНУцжБНЧзјБъЯЕжаЃЌOBдкxжсЩЯЃЌOB=4ЃЌOA=2![]() НЋШ§НЧаЮжНАхШЦдЕуOФцЪБеыа§зЊЃЌУПУыа§зЊ60ЁуЃЌдђЕк2019УыЪБЃЌЕуAЕФЖдгІЕуA Ёф ЕФзјБъЮЊЃЈ ЃЉ
НЋШ§НЧаЮжНАхШЦдЕуOФцЪБеыа§зЊЃЌУПУыа§зЊ60ЁуЃЌдђЕк2019УыЪБЃЌЕуAЕФЖдгІЕуA Ёф ЕФзјБъЮЊЃЈ ЃЉ
A. ЃЈЃ3ЃЌЃ![]() ЃЉB. ЃЈ3ЃЌЃ
ЃЉB. ЃЈ3ЃЌЃ![]() ЃЉC. ЃЈЃ3ЃЌ
ЃЉC. ЃЈЃ3ЃЌ![]() ЃЉD. ЃЈ0ЃЌ2
ЃЉD. ЃЈ0ЃЌ2![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФИЧзНкЧАЃЌФГЬдБІЕъДгГЇМвЙКНјФГПюЭјКьРёКаЃЌвбжЊИУПюРёКаУПИіГЩБОМлЮЊ30дЊЃЎОЪаГЁЕїВщЗЂЯжЃЌИУРёКаУПЬьЕФЯњЪлСПyЃЈИіЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉжЎМфТњзувЛДЮКЏЪ§ЙиЯЕЃЎЕБИУПюРёКаУПИіЪлМлЮЊ40дЊЪБЃЌУПЬьПЩТєГі300ИіЃЛЕБИУПюРёКаУПИіЪлМлЮЊ55дЊЪБЃЌУПЬьПЩТєГі150ИіЃЎ
ЃЈ1ЃЉЧѓyгыxжЎМфЕФКЏЪ§НтЮіЪНЃЈВЛвЊЧѓаДГіxЕФШЁжЕЗЖЮЇЃЉЃЛ
ЃЈ2ЃЉШєИУЕъРЯАхЯыДяЕНУПЬьВЛЕЭгк240ИіЕФЯњЪлСПЃЌдђИУРёКаУПИіЪлМлЖЈЮЊЖрЩйдЊЪБЃЌУПЬьЕФЯњЪлРћШѓзюДѓЃЌзюДѓРћШѓЪЧЖрЩйдЊ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЫцЛњГщШЁВПЗжбЇЩњЃЌОЭЁАбЇЯАЯАЙпЁБНјааЕїВщЃЌНЋЁАЖдздМКзіДэЬтНјааећРэЁЂЗжЮіЁЂИФе§ЁБЃЈбЁЯюЮЊЃККмЩйЁЂгаЪБЁЂГЃГЃЁЂзмЪЧЃЉЕФЕїВщЪ§ОнНјааСЫећРэЃЌЛцжЦГЩВПЗжЭГМЦЭМШчЯТЃК

ЧыИљОнЭМжааХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉИУЕїВщЕФбљБОШнСПЮЊ________ЃЌ ![]() =________%ЃЌ
=________%ЃЌ ![]() =________%ЃЌЁАГЃГЃЁБЖдгІЩШаЮЕФдВаФНЧЕФЖШЪ§ЮЊ__________ЃЛ
=________%ЃЌЁАГЃГЃЁБЖдгІЩШаЮЕФдВаФНЧЕФЖШЪ§ЮЊ__________ЃЛ
ЃЈ2ЃЉЧыФуВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉШєИУаЃга3200УћбЇЩњЃЌЧыФуЙРМЦЦфжаЁАзмЪЧЁБЖдДэЬтНјааећРэЁЂЗжЮіЁЂИФе§ЕФ
бЇЩњгаЖрЩйУћЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃКдкЦНааЫФБпаЮABCDЕФБпABЃЌCDЩЯНиШЁAFЃЌCEЃЌЪЙЕУAF=CEЃЌСЌНгEFЃЌЕуMЃЌNЪЧЯпЖЮEFЩЯСНЕуЃЌЧвEM=FNЃЌСЌНгANЃЌCMЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїAFNЁеЁїCEMЃЛ
ЃЈ2ЃЉШєЁЯCMF=107ЁуЃЌЁЯCEM=72ЁуЃЌЧѓЁЯNAFЕФЖШЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com