
 如图,在△ABC中,BE⊥AC,CF⊥AB,D为BC的中点.
如图,在△ABC中,BE⊥AC,CF⊥AB,D为BC的中点.分析 (1)根据直角三角形的性质证明即可;
(2)根据直角三角形斜边上的中线等于斜边的一半解答即可;
(3)根据等腰三角形的三线合一解答即可;
(4)根据线段垂直平分线的判定定理解答.
解答 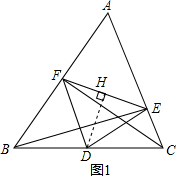 证明:(1)∵BE⊥AC,CF⊥AB,
证明:(1)∵BE⊥AC,CF⊥AB,
∴∠ABE+∠A=90°,∠ACF+∠A=90°,
∴∠ABE=∠ACF;
(2)∵BE⊥AC,CF⊥AB,D为BC的中点,
∴DF=$\frac{1}{2}$BC,DE=$\frac{1}{2}$BC,
∴DF=DE;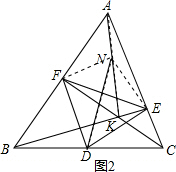 (3)如图1,∵DF=DE,DH⊥EF,
(3)如图1,∵DF=DE,DH⊥EF,
∴EH=FH;
(4)如图2,∵BE⊥AC,CF⊥AB,N为AK的中点,
∴NF=$\frac{1}{2}$AK,NE=$\frac{1}{2}$AK,
∴NF=NE,又DF=DE,
∴DN垂直平分EF.
点评 本题考查的是直角三角形的性质、等腰三角形的性质、线段垂直平分线的判定,掌握直角三角形斜边上的中线等于斜边的一半、与线段两端点的距离相等的点在线段的垂直平分线上.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:选择题
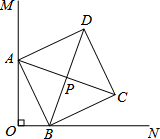 如图,∠MON=90°,点B在射线ON上且OB=2,点A在射线OM上,以AB为边在∠MON内部作正方形ABCD,其对角线AC、BD交于点P.在点A从O点出发,沿射线OM的运动过程中,下列说法正确的是( )
如图,∠MON=90°,点B在射线ON上且OB=2,点A在射线OM上,以AB为边在∠MON内部作正方形ABCD,其对角线AC、BD交于点P.在点A从O点出发,沿射线OM的运动过程中,下列说法正确的是( )| A. | 点P始终在∠MON的平分线上,且线段OP的长有最小值等于$\sqrt{2}$ | |
| B. | 点P始终在∠MON的平分线上,且线段OP的长有最大值等于$\sqrt{2}$ | |
| C. | 点P不一定在∠MON的平分线上,但线段OP的长有最小值等于$\sqrt{2}$ | |
| D. | 点P运动路径无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $({-\frac{3}{2},\frac{23}{4}})$ | B. | $({\frac{3}{2},\frac{23}{4}})$ | C. | $({\frac{3}{2},\frac{7}{2}})$ | D. | $({-\frac{3}{2},\frac{7}{2}})$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ,那么加上卡片上的数字;如果抽到的卡片形如
,那么加上卡片上的数字;如果抽到的卡片形如 ,那么减去卡片上的数字;②比较两人所抽4张卡片的计算结果,结果大的为胜者.小明抽到如图①所示的4张卡片,小丽抽到如图②所示的4张卡片,请你通过计算(要求有具体的计算过程),指出本次游戏的获胜者.
,那么减去卡片上的数字;②比较两人所抽4张卡片的计算结果,结果大的为胜者.小明抽到如图①所示的4张卡片,小丽抽到如图②所示的4张卡片,请你通过计算(要求有具体的计算过程),指出本次游戏的获胜者.
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y3 | D. | y2<y1<y3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com