
甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行.乙车出发2h休息.与甲车相遇.继续行驶.设甲、乙两车与B地的距离y(km)与行驶的时间x(h)之间的函数图象如图所示.
(1)写出甲车与B地的距离y(km)与行驶时间x(h)之间的函数关系式 _______
(2)乙车休息的时间为_________;
(3)写出休息前,乙车与B地的距离y(km)与行驶的时间x(h)之间的函数关系式___________;休息后,乙车与B地的距离y(km)与行驶的时间x(h)之间的函数关系式______;
(4)求行驶多长时间两车相距100km.

【考点】一次函数的应用.
【分析】(1)设甲车与B地的距离y(km)与行驶时间x(h)之间的函数关系式为y=kx+b,利用待定系数法解答即可;
(2)先把y=200代入甲的函数关系式中,可得x的值,再由图象可知乙车休息的时间;
(3)根据待定系数法,可得休息前,休息后,乙车与B地的距离y(km)与行驶的时间x(h)之间的函数关系式;
(4)分类讨论,0≤x≤2.5,y甲减y乙等于100千米,2.5≤x≤5时,y乙减y甲等于100千米即可.
【解答】解:(1)设甲车与B地的距离y(km)与行驶时间x(h)之间的函数关系式为y=kx+b,
可得: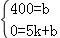 ,
,
解得: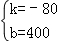 .
.
所以函数解析式为:y=﹣80x+400;
故答案为:y=﹣80x+400;
(2)把y=200代入y=﹣80x+400中,可得:200=﹣80x+400,
解得:x=2.5,
所以乙车休息的时间为:2.5﹣2=0.5小时;
故答案为:0.5小时;
(3)设休息前,乙车与B地的距离y(km)与行驶的时间x(h)之间的函数关系式为:y=kx,
∴200=2k,
∴k=100,
∴休息前,乙车与B地的距离y(km)与行驶的时间x(h)之间的函数关系式为:y=100x,
设休息后,乙车与B地的距离y(km)与行驶的时间x(h)之间的函数关系式为:y乙=kx+b,
y乙=kx+b图象过点(2.5,200),(5,400),
得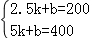 ,
,
解得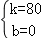 ,
,
乙车与甲车相遇后y乙与x的函数解 析式y乙=80x;
析式y乙=80x;
故答案为:y=100x,y乙=80x;
(4)设乙车与甲车相遇前y乙与x的函数解析式y乙=kx,图象过点(2,200),
解得k=100,
∴乙车与甲车相遇前y乙与x的函数解析式y乙=100x,
0≤x≤2.5,y甲减y乙等于100千米,
即400﹣80x﹣100x=100,解得 x=1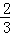 ;
;
2.5≤x≤5时,y乙减y甲等于100千米,
即2.5≤x≤5时,80x﹣(﹣80x+400)=100,解得x=3.125,
综上所述:x=1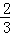 或x=3.125.
或x=3.125.
【点评】本题考查了一次函数的应用,待定系数法是求函数解析式的关键.


科目:初中数学 来源: 题型:
把两个含有45°角的直角三角板如图放置,点D在BC上,连结BE,AD,AD的延长线交BE于点F.试说明:
(1)△ACD与△BCE全等吗?请说明理由.
(2)AF与BE垂直吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(
 ,
,
 )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)求△PAC为直角三角形时点P的坐标.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com