练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．${x^2}-\frac{b}{a}x$+$\frac{{b}^{2}}{4{a}^{2}}$=（x-$\frac{b}{2a}$）2．

    分析 直接配上一次项系数的一半的平方，即可变为完全平方式．

    解答 解：${x^2}-\frac{b}{a}x$+$\frac{{b}^{2}}{4{a}^{2}}$=（x-$\frac{b}{2a}$）．
    故答案为：$\frac{{b}^{2}}{4{a}^{2}}$，$\frac{b}{2a}$．

    点评 本题考查了配方法的应用：配方法的理论依据是公式a2±2ab+b2=（a±b）2．二次三项式是完全平方式，则常数项是一次项系数一半的平方．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．已知关于x的方程3m-x=$\frac{1}{2}x+3$的解是x=4，求m2-2m+1的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

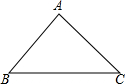    1．如图．张大爷家有一个三角形鱼塘，A，B，C三处分别栽有一棵树．现要扩大鱼塘面积，且将鱼塘改为圆形，并保留三棵树的位置不动，使鱼塘的面积最大，请你设计鱼塘的位置．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．如果x=$\frac{1}{2}$是关于x的方程2x2+3ax-2a=0的根，那么关于y的方程y2-3=a的解是（　　）
    A．±$\sqrt{5}$B．±1C．±2D．±$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

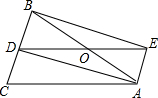    5．如图，△ABC中，AB=AC，AD是∠BAC的角平分线，点O是AB的中点，连接DO并延长到E，使DO=EO，连接AE，BE．
    （1）判断四边形AEBD是何特殊的四边形，并证明；
    （2）当∠BAC为多少度时，四边形AEBD是正方形？并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．方程mx2-4x+1=0（m＜0）的根是（　　）
    A．$\frac{1}{4}$B．$\frac{{2±\sqrt{4-m}}}{m}$C．$\frac{{2±2\sqrt{4-m}}}{m}$D．$\frac{{2±m\sqrt{4-m}}}{m}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．关于x的一元二次方程$\sqrt{2}{x^2}+\sqrt{2}{a^2}=3ax$的两根应为（　　）
    A．$\frac{{-\sqrt{2}±a}}{{\sqrt{2}}}$B．$\sqrt{2}a$，$\frac{{\sqrt{2}}}{2}a$C．$\frac{{2±\sqrt{2}a}}{4}$D．$±\sqrt{2}a$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．用适当方法解下列方程
    （1）6x2-x-2=0
    （2）（x+3）（x-3）=3
    （3）x2-2mx+m2-n2=0
    （4）12a2x2-5ax+2=0（a≠0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．如图，△ABC∽△DEF，若∠B=50°，则∠E的度数是50度．

    查看答案和解析>>

    同步练习册答案