
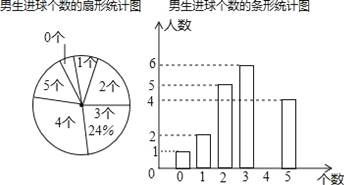
����Ŀ��Ϊ�˽⡰�����У�����չ�����ij��ѧ���������ν����˶������Ų��ԣ�ÿ������5�Σ����а༶���Խ����������ȡ��ij��ѧ�������������Ϊ�������Խ���������������������˲�������ͳ��ͼ�����ð�Ů����22�ˣ�Ů���������������Ϊ2����λ��Ϊ3��
Ů�����������ͳ�Ʊ�
������������ | ���� |
0 | 1 |
1 | 2 |
2 | x |
3 | y |
4 | 4 |
5 | 2 |
��1��������༶������������
��2����ȫ����ͳ��ͼ�������������ͳ��ͼ�н�2��������ε�Բ�ĽǶ�����
��3����У����ѧ��1880�ˣ��������ȫУ������������3����ѧ����Լ��_____�ˣ�
���𰸡�25
����������1�����ݽ�����Ϊ3������������ռ�İٷֱ�����������������ɣ�
��2�����������Ϊ4�����������Լ�������Ϊ2����Բ�ĽǶ�������ȫ����ͳ��ͼ���ɣ�
��3�����������������3���İٷֱȣ�����1880���ɵõ������
�⣺��1������༶����������Ϊ6��24%=25���ˣ���
������༶����������Ϊ25�ˣ�
��2������������Ϊ4��������Ϊ25����1+2+5+6+4��=7���ˣ�����2���������Բ�ĽǶ���Ϊ360���![]() =72�㣻
=72�㣻
��ȫ����ͳ��ͼ����ͼ��ʾ��
��3����������ã�47��ѧ����Ů���������Ϊ6+4+2=12������������Ϊ6+7+4=17��
��1880��![]() =1160���ˣ���
=1160���ˣ���
��ȫУ������������3����ѧ����Լ��1160�ˣ�
�ʴ�Ϊ��1160��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
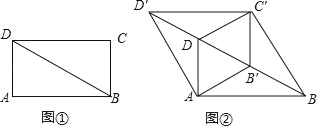
����Ŀ����ͼ�٣�BD�Ǿ���ABCD�ĶԽ��ߣ���ABD=30�㣬AD=1������BCD������BD����ƽ�Ƶ���B'C'D'��λ�ã�ʹB'ΪBD�е㣬����AB'��C'D��AD'��BC'����ͼ�ڣ�
��1����֤���ı���AB'C'D�����Σ�
��2���ı���ABC'D����ܳ�Ϊ�� ����
��3�����ı���ABC'D'�����������Խ��������õõ����ĸ�������ƴ�����������ȵľ��Σ�ֱ��д�����п���ƴ�ɵľ����ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ε��ܳ�Ϊ 13cm������һ�߳�Ϊ 3cm����õ��������εĵױ߳�Ϊ����
A. 7 B. 3 C. 7 �� 3 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�˹��������Լ�õ磬���÷ֶμƷѵķ������¼���ÿ����ͥ�ĵ�ѣ����õ���������200��ʱ����0.55Ԫ/�ȼƷѣ����õ�������200��ʱ�����е�200����0.55Ԫ/�ȼƷѣ��������ְ�0.70Ԫ/�ȼƷѣ���ÿ����ͥ���õ���Ϊx��ʱ��Ӧ�����yԪ��
��1���ֱ����0��x��200��x��200ʱ��y��x�ĺ�������ʽ��
��2��С����5�·ݽ��ɵ��117Ԫ��С����������õ���ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A������Ϊ����8��0������P������Ϊ��-![]() ��0����ֱ��y=
��0����ֱ��y=![]() x+b����A����y���ڵ�B���Ե�PΪԲ�ģ���PAΪ�뾶��Բ��x���ڵ�C��
x+b����A����y���ڵ�B���Ե�PΪԲ�ģ���PAΪ�뾶��Բ��x���ڵ�C��
��1���жϵ�B�Ƿ��ڡ�P�ϣ�˵�����ɣ�
��2�����A��B��C����������ߵĽ���ʽ���������������P����һ������ΪD�����꣮
��3����P���Ƿ����һ��Q��ʹ��A��P��B��QΪ������ı��������Σ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̽����
��ͼ1����ACB�͡�DCE��Ϊ�ȱ������Σ���A��D��E��ͬһֱ���ϣ�����BE��
��1��֤����AD=BE��
��2�����AEB�Ķ�����
�����ʽ��
��ͼ2����ACB�͡�DCE��Ϊ����ֱ�������Σ���ACB=��DCE=90�㣬��A��D��E��ͬһֱ���ϣ�CMΪ��DCE��DE���ϵĸߣ�����BE���������AEB�Ķ����Լ��ж��߶�CM��AE��BE֮���������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����߾���A��1��0����B��0��3�����㣬�Գ�����x=��1��
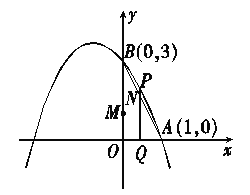
��1���������߶�Ӧ�ĺ�����ϵʽ��
��2������Ѵӵ�O��������ÿ��1����λ���ȵ��ٶ����߶�OA���˶���ͬʱ����M��O�������ÿ��3����λ���ȵ��ٶ����߶�OB���˶����������x��Ĵ��߽��߶�AB�ڵ�N�����������ڵ�P�����˶���ʱ��Ϊt��
����tΪ��ֵʱ���ı���OMP��Ϊ���Σ�
�ڡ�AON�ܷ�Ϊ���������Σ����ܣ����t��ֵ�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������˵���У���ȷ������ ��
A���������������ȫ�ȣ������DZ��ǹ���ֱ�߳���ԳƵ�ͼ��
B��������������ι���ijֱ�߳���Գƣ���ô������ȫ��������
C�������������ǹ��ڵױ����߳���ԳƵ�ͼ��
D��һ���߶��ǹ��ھ������߶��е��ֱ�߳���ԳƵ�ͼ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com