
【题目】问题探究:
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
(1)证明:AD=BE;
(2)求∠AEB的度数.
问题变式:
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请求出∠AEB的度数以及判断线段CM、AE、BE之间的数量关系,并说明理由.

【答案】探究展示:(1)证明见解析; (2)600.
拓展延伸:(1)∠AEB=900 ;(2)AE= 2CM+BE,理由见解析.
【解析】试题分析:问题探究:(1)先证出∠ACD=∠BCE,那么△ACD≌△BCE,根据全等三角形证出AD=BE;
(2)∠ADC=∠BEC,求出∠ADC=120°,得出∠BEC=120°,从而证出∠AEB=60°;
问题变式:证明△ACD≌△BCE,得出∠ADC=∠BEC、AD=BE,从而得到∠AEB的度数,再由等腰直角三角形的性质得到DM=ME=CM即可.
试题解析:问题探究:
(1) ∵△ACB和△DCE均为等边三角形,∴∠ACB=∠DCE=60°,AC=BC、DC=EC,∴∠ACD=∠BCE,∴△CDA≌△CEB, ∴AD=BE
(2)∵△CDA≌△CEB,∴∠CEB=∠CDA=1200,又∠CED=600,∴∠AEB=1200-600=600.
问题变式:
(1)∵△ACB和△DCE均为等腰直角三角形,∠ACB =∠DCE= 900,
∴AC=BC, CD=CE,
∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD= ∠BCE
∴△ACD≌△BCE
∴AD = BE, ∠BEC=∠ADC=1350.
∴∠AEB=∠BEC-∠CED=1350-450=900
(2)AE= 2CM+BE
在等腰直角三角形DCE中,CM为斜边DE上的高,
∴CM= DM= ME,∴DE=2CM.
∴AE=DE+AD=2CM+BE
∴AE= 2CM+BE


科目:初中数学 来源: 题型:
【题目】某蓄水池的横断面示意图如图所示,分深水区和浅水区,如果这个注满水的蓄水池以固定的流量把水全部放出,下面的图象能大致表示水的深度h和放水时间t之间的关系的是( )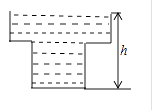
A.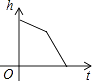
B.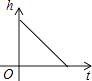
C.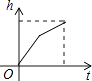
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
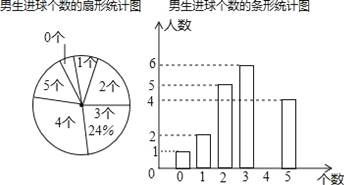
【题目】为了解“足球进校园”活动开展情况,某中学利用体育课进行了定点射门测试,每人射门5次,所有班级测试结束后,随机抽取了某班学生的射门情况作为样本,对进球的人数进行整理后,绘制了不完整的统计图表,该班女生有22人,女生进球个数的众数为2,中位数为3.
女生进球个数的统计表
进球数(个) | 人数 |
0 | 1 |
1 | 2 |
2 | x |
3 | y |
4 | 4 |
5 | 2 |
(1)求这个班级的男生人数;
(2)补全条形统计图,并计算出扇形统计图中进2个球的扇形的圆心角度数;
(3)该校共有学生1880人,请你估计全校进球数不低于3个的学生大约有_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由完全平方公式可知:32+2×3×5+52=(3+5)2=64,用这一方法计算:1.23452+2.469×0.7655+0.76552= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB的后面有一办公楼CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高3米的影子CE;而当光线与地面的夹角是45°时,教学楼顶A在地面上的影子F与墙角C有30米的距离(B、F、C在一条直线上).现要在A、E之间挂一些彩旗,求A、E之间的距离.(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() ,精确到0.1m)
,精确到0.1m)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com