
【题目】如图,点A的坐标为(﹣8,0),点P的坐标为(-![]() ,0),直线y=
,0),直线y=![]() x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.
x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.
(1)判断点B是否在⊙P上?说明理由.
(2)求过A、B、C三点的抛物线的解析式;并求抛物线与⊙P另外一个交点为D的坐标.
(3)⊙P上是否存在一点Q,使以A、P、B、Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.

【答案】⑴点B在⊙P上,理由见解析;⑵抛物线的解析式为![]() ,D
,D![]()
⑶⊙P上不存在点Q,使以A、P、B、Q为顶点的四边形,理由见解析.
【解析】试题分析:(1)通过计算PB与PA是否相等即可做出判断;
(2)由圆的性质确定出点C的坐标,然后利用待定系数法即可解决;
(3)分AB为菱形的对角线, AB、AP为菱形的邻边,AB、BP为菱形的邻边, 三种情况进行讨论.
试题解析:⑴∵A(-8,0)在直线![]() 上,则有b=6
上,则有b=6
∴点B(0,6),即OB=6,
在Rt△BOP中,由勾股定理得PB=![]() ,则PB=PA,∴点B在⊙P上.
,则PB=PA,∴点B在⊙P上.
⑵AC=2PA=![]() ,则OC=
,则OC=![]() ,点C
,点C![]() ,抛物线过点A、C,则设所求抛物线为
,抛物线过点A、C,则设所求抛物线为![]() ,代入点C
,代入点C![]() ,则有a=
,则有a=![]() ,
,
抛物线的解析式为![]() ,
,
直线x=![]() 是抛物线和圆P的对称轴,点B的对称点为D,由对称可得D
是抛物线和圆P的对称轴,点B的对称点为D,由对称可得D![]() .
.
⑶当点Q在⊙P上时,有PQ=PA=![]() ,
,
如图1所示,假设AB为菱形的对角线,那么PQ⊥AB且互相平分,由勾股定理得PE=![]() ,则2PE≠PQ,所以四边形APBQ不是菱形.
,则2PE≠PQ,所以四边形APBQ不是菱形.
如图2所示,假设AB、AP为菱形的邻边,则AB≠AP,所以四边形APQB不是菱形.
如图3所示,假设 AB、BP为菱形的邻边,则AB≠BP,所以四边形AQPB不是菱形.
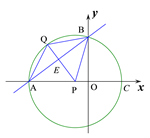
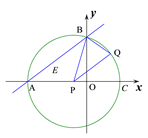
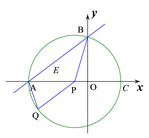
图1 图2 图3
综上所述,⊙P上不存在点Q,使以A、P、B、Q为顶点的四边形.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
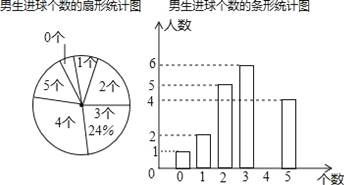
【题目】为了解“足球进校园”活动开展情况,某中学利用体育课进行了定点射门测试,每人射门5次,所有班级测试结束后,随机抽取了某班学生的射门情况作为样本,对进球的人数进行整理后,绘制了不完整的统计图表,该班女生有22人,女生进球个数的众数为2,中位数为3.
女生进球个数的统计表
进球数(个) | 人数 |
0 | 1 |
1 | 2 |
2 | x |
3 | y |
4 | 4 |
5 | 2 |
(1)求这个班级的男生人数;
(2)补全条形统计图,并计算出扇形统计图中进2个球的扇形的圆心角度数;
(3)该校共有学生1880人,请你估计全校进球数不低于3个的学生大约有_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图:

(1)本次被调查的学生有 名;
(2)补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;
(3)该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形.请解答下列问题:
(1)写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称;
(2)探究:当等对角线四边形中两条对角线所夹锐角为60°时,这对60°角所对的两边之和与其中一条对角线的大小关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com