
【题目】1876年,美国总统Garfield用如图所示的两个全等的直角三角形证明了勾股定理,若图中![]() ,
,![]() ,
,![]() ,则下面结论错误的是( )
,则下面结论错误的是( )
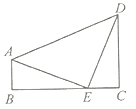
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() 是等腰直角三角形
是等腰直角三角形
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),与x轴的另一个交点在点(1,0)和(2,0)之间,对称轴l如图所示,则下列结论:①abc>0;②a﹣b+c=0;③a+c>0;④2a+c<0,其中正确的结论个数是( )
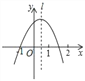
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
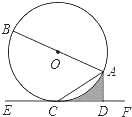
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点C在线段AB上,AC=2BC,点D、E在直线AB上,点D在点E的左侧
(1)若AB=18,DE=8,线段DE在线段AB上移动
①如图1,当E为BC中点时,求AD的长;
②点F(异于A,B,C点)在线段AB上,AF=3AD,CE+EF=3,求AD的长;
(2)若AB=2DE,线段DE在直线AB上移动,且满足关系式![]() ,则
,则![]() ______.
______.
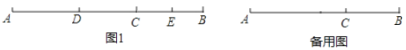
查看答案和解析>>
科目:初中数学 来源: 题型:
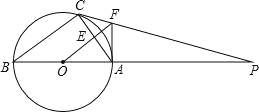
【题目】如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC,交AC于点E,交PC于点F,连接AF.
(1)求证:AF是⊙O的切线;
(2)已知⊙O的半径为4,AF=3,求线段AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
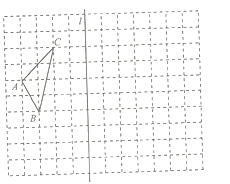
【题目】如图,在![]() 的正方形网格中,
的正方形网格中,![]() 是格点三角形,点
是格点三角形,点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .
.
(1)在图中画出相应的平面直角坐标系;
(2)画出![]() 关于直线
关于直线![]() 对称的
对称的![]() ,并标出点
,并标出点![]() 的坐标;
的坐标;
(3)若点![]() 在
在![]() 内,其关于直线
内,其关于直线![]() 的对称点是
的对称点是![]() ,则
,则![]() 的坐标是 .
的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
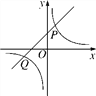
【题目】如图,直线y=k1x+1与双曲线y=![]() 相交于P(1,m),Q(-2,-1)两点.
相交于P(1,m),Q(-2,-1)两点.
(1)求m的值;
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上三点,且x1<x2<0<x3,请直接说明y1,y2,y3的大小关系;
(3)观察图象,请直接写出不等式k1x+1>![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
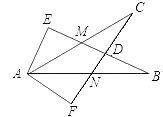
【题目】如图,已知∠E=∠F,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有( )
A. 1个B. 2个
C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和.如23=3+5,33=7+9+11,43=13+15+17+19,…,若m3“分裂”后,其中有一个奇数是347,则m的值是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com