
【题目】如图,四边形![]() 中,AD∥BC,点
中,AD∥BC,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上,![]() ,过点
,过点![]() 、
、![]() 分别作
分别作![]() 的垂线,垂足为
的垂线,垂足为![]() 、
、![]() .
.

(1)求证:△AGE≌△CHF;
(2)连接![]() ,线段
,线段![]() 与
与![]() 请交于点M,若CH=4,GH=10,求△AGM的面积.
请交于点M,若CH=4,GH=10,求△AGM的面积.
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm.动点P、Q分别从点A、B同时开始移动,点P的速度为1 cm/秒,点Q的速度为2 cm/秒,点Q移动到点C后停止,点P也随之停止运动下列时间瞬间中,能使△PBQ的面积为15cm 的是( )
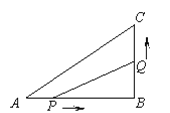
A. 2秒钟 B. 3秒钟 C. 4秒钟 D. 5秒钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.有下列结论:
①∠DEO=45°;
②△AOD≌△COE;
③S四边形CDOE=![]() S△ABC;
S△ABC;
④![]() .
.
其中正确的结论序号为 .(把你认为正确的都写上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, AD是![]() 的中线,E,F分别是AD和AD延长线上的点,且
的中线,E,F分别是AD和AD延长线上的点,且![]() ,连结BF,CE.下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有________(填上正确的序号)
,连结BF,CE.下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有________(填上正确的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学六七年级有350名同学去春游,已知2辆A型车和1辆B型车可以载学生100人;1辆A型车和2辆B型车可以载学生110人.
(1)A、B型车每辆可分别载学生多少人?
(2)若租一辆A需要100元,一辆B需120元,请你设计租车方案,使得恰好运送完学生并且租车费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,AD=2,AB=2![]() ,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.
,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.
(1)求∠ABE的大小及弧DEF的长度;
(2)在BE的延长线上取一点G,使得弧DE上的一个动点P到点G的最短距离为2![]() -2,求BG的长.
-2,求BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的周长是20,OB和OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是( )

A. 20 B. 25 C. 30 D. 35
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com