
【题目】如图, AD是![]() 的中线,E,F分别是AD和AD延长线上的点,且
的中线,E,F分别是AD和AD延长线上的点,且![]() ,连结BF,CE.下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有________(填上正确的序号)
,连结BF,CE.下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有________(填上正确的序号)

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:
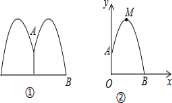
【题目】如图是某公园一圆形喷水池,水流在各个方向沿形状相同的抛物线落下,建立如下图所示的坐标系,如果喷头所在处A(0,1.25),水流路线最高处M(1,2.25),则该抛物的解析式为__________________________。如果不考虑其他因素,那么水池的半径至少要______m,才能使喷出的水流不至落到池外.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出的速度保持不变).该仓库库存物资W(吨)与时间t(小时)之间的函数关系如图所示.则这批物资从开始调进到全部调出所需要的时间是( )

A. 8.4小时 B. 8.6小时 C. 8.8小时 D. 10小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 中,AD∥BC,点
中,AD∥BC,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上,![]() ,过点
,过点![]() 、
、![]() 分别作
分别作![]() 的垂线,垂足为
的垂线,垂足为![]() 、
、![]() .
.

(1)求证:△AGE≌△CHF;
(2)连接![]() ,线段
,线段![]() 与
与![]() 请交于点M,若CH=4,GH=10,求△AGM的面积.
请交于点M,若CH=4,GH=10,求△AGM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小辉从家(点0)出发,沿着等腰三角形A0B的边0A-AB-B0的路径去匀匀速散步,其中0A=0B。设小辉距家(点0)的距离为S,散步的时间为t,则下列图形中能大致刻画S与t之间函数关系的图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠ACB=90°,AC=BC,AE 是 BC 边的中线,过点C 作 CF⊥AE,垂足为点 F,过点 B 作 BD⊥BC 交 CF 的延长线于点 D.
(1)试证明:AE=CD;
(2)若 AC=12cm,求线段 BD 的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com