
【题目】![]() 中,
中,![]() ,点
,点![]() 、
、![]() 、
、![]() 分别在
分别在![]() 、
、![]() 、
、![]() 上,
上,![]() .
.
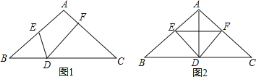
![]() 如图
如图![]() ,求证:
,求证:![]()
![]() 为
为![]() 中点如图
中点如图![]() ,连接
,连接![]() .
.
①求证:![]() 平分
平分![]() ;
;
②若四边形![]() 为菱形,求
为菱形,求![]() 的度数及
的度数及![]() 的值.
的值.
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】 某学校为了了解九年级学生的体能情况,抽取了部分学生进行了体能测试,学生的测试成绩分四类:A:优秀;B:良好;C:合格;D不合格,将抽测学生的成绩绘制成如下两幅不完整的统计图,请根据统计图解答下列问题:
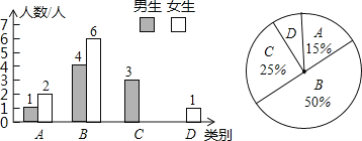
(1)求本次调查的学生总人数;
(2)成绩为C的女生有______人,成绩为D的男生有______人;
(3)扇形统计图中成绩为D的学生所对应的扇形的圆心角度数为______;
(4)补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
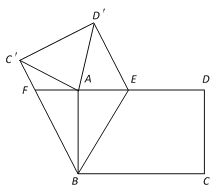
【题目】如图,在矩形ABCD中,AB=4,AD=6,E是AD边上的一个动点,将四边形BCDE沿直线BE折叠,得到四边形BC′D′E,连接AC′,AD′.
(1)若直线DA交BC′于点F,求证:EF=BF;
(2)当AE=![]() 时,求证:△AC′D′是等腰三角形;
时,求证:△AC′D′是等腰三角形;
(3)在点E的运动过程中,求△AC′D′面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
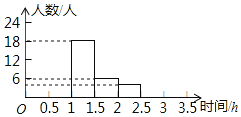
【题目】为减轻学生的作业负担,某地教育局规定初中阶段学生每晚的作业量不超过1.5小时,一个月后,九年一班芳芳对本班每位同学晚上作业时间进行了一次调查,并根据收集的数据绘制了如图所示的不完整的频数分布直方图(每组包含最大值,不包含最小值),并知1﹣1.5h占45%,2~2.5h占10%,请根据以上信息解答问题.
(1)求该班共有多少名学生;
(2)求该班作业时间不超过1小时和超过2.5小时的共有多少人;
(3)若该市九年级共有3000名学生,请估计他们中完成作业超过1.5小时而不超过2.5小时的有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
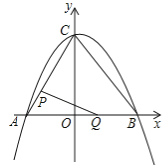
【题目】如图①,在平面直角坐标系中,二次函数y=![]() x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
(1)填空:b= ,c= ;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)点M在抛物线上,且△AOM的面积与△AOC的面积相等,求出点M的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】碑林书法社小组用的书法练习纸(毛边纸可以到甲商店购买,也可以到乙商店购买已知两商店的标价都是每刀20元(每刀100张),但甲商店的优惠条件是:若购买不超过10刀,则按标价买,购买10以上,从第11刀开始按标价的七折卖;乙商店的优惠条件是:购买一只9元的毛笔,从第一刀开始按标价的八五折卖.购买刀数为![]() (刀),在甲商店购买所需费用为
(刀),在甲商店购买所需费用为![]() 元,在乙商店购买所需费用为
元,在乙商店购买所需费用为![]() 元.
元.
(1)写出![]() 、
、![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(2)求在乙商店购买所需总费用小于甲商店购买所需总费用时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
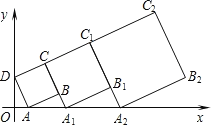
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2019个正方形的面积是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长均为1的方格纸中,线段AB的端点A、B均在小正方形的顶点上.
(1)在方格纸中画出以AB为一条直角边的等腰直角△ABC,顶点C在小正方形的顶点上;
(2)在方格纸中画出△ABC的中线BD,将线段DC绕点C顺时针旋转90°得到线段CD′,画出旋转后的线段CD′,连接BD′,直接写出四边形BDCD′的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
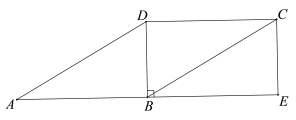
【题目】如图,在□ABCD中,∠ABD=90°,延长AB至点E,使BE=AB,连接CE.
(1)求证:四边形BECD是矩形;
(2)连接DE交BC于点F,连接AF,若CE=2,∠DAB=30°,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com