Question

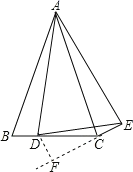
【题目】如图，△ABC中，AB=AC，点D为BC上一点，以AD为腰作等腰△ADE，且AD=AE， ∠BAC=∠DAE=30°，连接CE,若BD=2,S△DCE=，则CD的长为 ______.

Answer 1

【答案】

【解析】

过D作DF⊥EC交EC的延长线于F，易证△ABD≌△ACE，得到∠ACE=∠B，根据∠BAC=30°，于是得到∠B+∠ACB=150°，等量代换得到∠BCE=∠ACB+∠ACE=150°，由邻补角的性质得到∠DCF=30°，根据直角三角形的性质得到DF=CD，根据△DCE的面积为，列方程即可得到结论．

过D作DF⊥EC交EC的延长线于F，如图，

∵∠BAC=∠DAE，

∴∠BAC∠DAC=∠DAE∠DAC，

∴∠BAD=∠EAC，

在△ABD和△ACE中，

AB=AC，∠BAD=∠EAC，AD=AE，

∴△ABD≌△ACE(SAS)，

∴∠ACE=∠B，BD=CE

∵∠BAC=30°，

∴∠B+∠ACB=150°，

∴∠BCE=∠ACB+∠ACE=150°，

∴∠DCF=30°，

∴DF=CD，

∵CE=BD，△DCE的面积为1，

∴CEDF=BDCD ==，

∴CD=

故答案为：.