
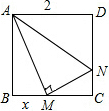
 正方形ABCD边长为2,M、N分别为BC、CD上的点,AM⊥MN,BM=x,求x为何值时,△ABM∽△AMN?
正方形ABCD边长为2,M、N分别为BC、CD上的点,AM⊥MN,BM=x,求x为何值时,△ABM∽△AMN?| AB |
| BM |
| AM |
| MN |
| 2 |
| 2-x |
| x |
| CN |
| x(2-x) |
| 2 |
| x(2-x) |
| 2 |
| (2-x)2(x2+4) |
| 4 |
| AB |
| BM |
| AM |
| MN |
| AB2 |
| BM2 |
| AM2 |
| MN2 |
| 4 |
| x2 |
| 4+x2 | ||
|


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com