
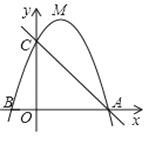
【题目】如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
(1)求抛物线的表达式;
(2)在直线AC的上方的抛物线上,有一点P(不与点M重合),使△ACP的面积等于△ACM的面积,请求出点P的坐标;
【答案】(1)![]() ;(2)P(2,3).
;(2)P(2,3).
【解析】
(1)抛物线的表达式为![]() ,即可求解;
,即可求解;
(2)过点M做直线m∥AC,直线m与抛物线的交点即为点P.
解:(1)∵y=ax2+bx+3与x轴交于A(3,0),B(﹣1,0)两点,
设抛物线解析式为:![]()
∴![]() 解得
解得![]()
∴抛物线的表达式为:![]()
(2)由(1)得抛物线的表达式为:![]()
∴顶点M的坐标为(1,4),点C坐标为(0,3)
设直线AC的解析式为:![]() ,把A(3,0)和C(0,3)代入得
,把A(3,0)和C(0,3)代入得
![]() 解得
解得![]()
∴直线AC的解析式为:![]()
过点M做直线m∥AC,直线m与抛物线的交点即为点P,
等底同高使△ACP的面积等于△ACM的面积.
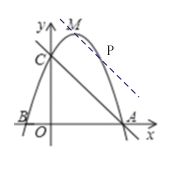
设直线m的表达式为:![]() ,
,
将M(1,4)代入得:b=5
∴直线m的表达式为:![]()
∴联立方程组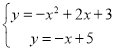 解得
解得![]()
![]()
∵点P不与点M重合
∴![]() 舍去
舍去
∴点P坐标为(2,3).
故答案为:(1)![]() ;(2)P(2,3).
;(2)P(2,3).


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】小华和小丽设计了A、B两种游戏:游戏A的规则是:用3张数字分别是2、3、4的扑克牌,将牌洗匀后背面朝上放置在桌面上,第一次随机抽出一张牌记下数字后再原样放回,洗匀后再第二次随机抽出一张牌记下数字,若抽出的两张牌上的数字之和为偶数,则小华获胜;若两数字之和为奇数,则小丽获胜.游戏B的规则是:用4张数字分别是5、6、8、8的扑克牌,将牌洗匀后背面朝上放置在桌面上,小华先随机抽出一张牌,抽出的牌不放回,小丽从剩下的牌中再随机抽出一张牌,若小华抽出的牌面上的数字比小丽抽出的牌面上的数字大,则小华获胜,否则小丽获胜.请你帮小丽选择其中一种游戏,使她获胜的可能性较大,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某体育用品商店,购买30根跳绳和60个毽子共用720元,购买10根跳绳和50个毽子共用360元.
(1)跳绳、毽子的单价各是多少元?
(2)该店在“五四”青年节期间开展促销活动,所有商品按同样的折数打折销售.节日期间购买100根跳绳和100个毽子只需1800元,该店的商品按原价的几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举行钢笔书法大赛,对各年级同学的获奖情况进行了统计,并绘制了如下两幅不完整的统计图.
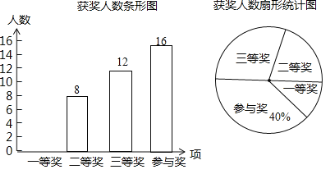
请结合图中相关信息解答下列问题:
(1)扇形统计图中三等奖所在扇形的圆心角的度数是______度;
(2)请将条形统计图补全;
(3)获得一等奖的同学中有![]() 来自七年级,有
来自七年级,有![]() 来自九年级,其他同学均来自八年级.现准备从获得一等奖的同学中任选2人参加市级钢笔书法大赛,请通过列表或画树状图的方法求所选出的2人中既有八年级同学又有九年级同学的概率.
来自九年级,其他同学均来自八年级.现准备从获得一等奖的同学中任选2人参加市级钢笔书法大赛,请通过列表或画树状图的方法求所选出的2人中既有八年级同学又有九年级同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学决定开展课后服务活动,学校就“你最想开展哪种课后服务项目”问题进行了随机问卷调查,调查分为四个类别:![]() .舞蹈;
.舞蹈;![]() .绘画与书法;
.绘画与书法;![]() .球类;
.球类;![]() .不想参加.现根据调查结果整理并绘制成如下不完整的扇形统计图和条形统计图,请结合图中所给信息解答下列问题:
.不想参加.现根据调查结果整理并绘制成如下不完整的扇形统计图和条形统计图,请结合图中所给信息解答下列问题:
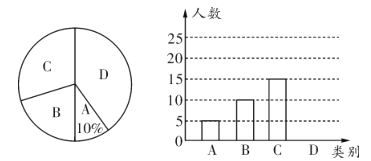
(1)这次统计共抽查了_________名学生,请补全条形统计图;
(2)该校共有600名学生,根据以上信息,请你估计全校学生中想参加![]() 类活动的人数;
类活动的人数;
(3)若甲、乙两名同学,各自从![]() 三个项目中随机选一个参加,请用列表或画树状图的方法求他们选中同一项目的概率.
三个项目中随机选一个参加,请用列表或画树状图的方法求他们选中同一项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,∠A=30°,∠B=90°,AC=8,点 D 在边 AB, 且 BD=![]() ,点 P 是△ABC 边上的一个动点,若 AP=2PD 时,则 PD的长是____________.
,点 P 是△ABC 边上的一个动点,若 AP=2PD 时,则 PD的长是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】赣南脐橙果大形正,肉质脆嫩,风味浓甜芳香,深受大家的喜爱.某脐橙生产基地生产的礼品盒包装的脐橙每箱的成本为30元,按定价50元出售,每天可销售200箱.为了增加销量,该生产基地决定采取降价措施,经市场调研,每降价1元,日销售量可增加20箱.


(1)求出每天销售量y(箱)与销售单价x(元)之间的函数关系式;
(2)若该生产基地每天要实现最大销售利润,每箱礼品盒包装的脐橙应定价多少元?每天可实现的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=![]() (x-h)2+k的顶点在x轴上,其对称轴与直线y=x交于点A(1,1),点P是抛物线上一点,以P为圆心,PA长为半径画圆,⊙P交x轴于B、C两点.
(x-h)2+k的顶点在x轴上,其对称轴与直线y=x交于点A(1,1),点P是抛物线上一点,以P为圆心,PA长为半径画圆,⊙P交x轴于B、C两点.
⑴h= ,k= ;
⑵①当点P在顶点时,BC= ;
②BC的值是否随P点横坐标的变化而变化?如果变化,请说明理由,如果不变化,请求出这个值.
查看答案和解析>>
科目:初中数学 来源: 题型:
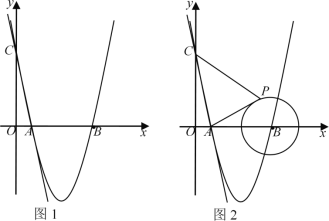
【题目】如图1,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴的另一个交点为
轴的另一个交点为![]() .
.
(1)求抛物线的解析式及![]() 点坐标;
点坐标;
(2)若点M为x轴下方抛物线上一动点,连接MA、MB、BC,当点M运动到某一位置时,四边形AMBC面积最大,求此时点M的坐标及四边形AMBC的面积;
(3)如图2,若![]() 点是半径为2的⊙
点是半径为2的⊙![]() 上一动点,连接
上一动点,连接![]() 、
、![]() ,当点
,当点![]() 运动到某一位置时,
运动到某一位置时,![]() 的值最小为_________.(直接写出结果)
的值最小为_________.(直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com