
(1)证明:在BC上取点E,使BD=DE,
∵AD⊥BC,
∴AB=AE,
∴∠AEB=∠ABC=2∠C,
∴∠C=∠EAC
∴EC=EA=AB,
∴CD=DE+EC=BD+AB
(2)解:由(1)得:
∵a
2-4bc=(b+c)
2-4bc=(b-c)
2又c>b,即c≠b,
∴(b-c)
2>0,
∴方程x
2-ax+bc=0有两个不相等的实数根.
(3)解:设方程的两根为k,2k,
代入得k
2-ak+bc=0①及4k
2-2ak+bc=0②,
由②-4×①得k=

,代入①得(

)
2-a•

+bc=0,
化简得9bc=2a
2,
又∵a
2=(b+c)
2代入得2b
2-5bc+2c
2=0,(2b-c)(b-2c)=0,
∵b<c,
∴c=2b
∵AD⊥BC,
∴∠B=60°,
∴∠C=30°,
∴∠BAC=90°,
∴△ABC为直角三角形.
分析:(1)在BC上取点E,使BD=DE,推出AB=AE=EC,从而推出CD=BD+AB;
(2)计算出根的判别式,通过配方及(1)中结论,证出根的判别式大于0,从而判定方程有两个不相等的实数根;
(3)设方程的两根为k,2k,代入得k
2-ak+bc=0①及4k
2-2ak+bc=0②,求出c=2b,再根据∠B=60°,∠C=30°,∠BAC=90°,证出△ABC为直角三角形.
点评:本题考查了根的判别式、根与系数的关系、等腰三角形的判定与性质,作出辅助线AE=AB是解题的关键.

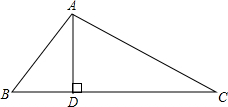 如图,△ABC中,AD⊥BC于D,∠B=2∠C.
如图,△ABC中,AD⊥BC于D,∠B=2∠C. (1)证明:在BC上取点E,使BD=DE,
(1)证明:在BC上取点E,使BD=DE, ,代入①得(
,代入①得( )2-a•
)2-a• +bc=0,
+bc=0,

 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.