

分析 (1)根据等边三角形的性质,利用SAS证明△ABQ≌△CAP即可;
(2)先判定△ABQ≌△CAP,根据全等三角形的性质可得∠BAQ=∠ACP,从而得到∠QMC=60°;
(3)先判定△ABQ≌△CAP,根据全等三角形的性质可得∠BAQ=∠ACP,从而得到∠QMC=120°.
解答  解:(1)证明:如图1,∵△ABC是等边三角形
解:(1)证明:如图1,∵△ABC是等边三角形
∴∠ABQ=∠CAP=60°,AB=CA,
又∵点P、Q运动速度相同,
∴AP=BQ,
在△ABQ与△CAP中,
$\left\{\begin{array}{l}{AB=CA}\\{∠ABQ=∠CAP}\\{AP=BQ}\end{array}\right.$,
∴△ABQ≌△CAP(SAS);
(2)点P、Q在AB、BC边上运动的过程中,∠QMC不变.
理由:∵△ABQ≌△CAP,
∴∠BAQ=∠ACP,
∵∠QMC是△ACM的外角,
∴∠QMC=∠ACP+∠MAC=∠BAQ+∠MAC=∠BAC
∵∠BAC=60°,
∴∠QMC=60°;
(3)如图2,点P、Q在运动到终点后继续在射线AB、BC上运动时,∠QMC不变.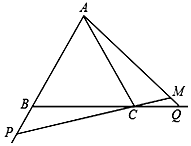
理由:同理可得,△ABQ≌△CAP,
∴∠BAQ=∠ACP,
∵∠QMC是△APM的外角,
∴∠QMC=∠BAQ+∠APM,
∴∠QMC=∠ACP+∠APM=180°-∠PAC=180°-60°=120°,
即若点P、Q在运动到终点后继续在射线AB、BC上运动,∠QMC的度数为120°.
点评 此题是三角形综合题,主要考查了等边三角形的性质、全等三角形的判定与性质等知识的综合应用.解决问题的关键是掌握全等三角形的判定方法:两边及其夹角分别对应相等的两个三角形全等.解题时注意运用全等三角形的对应边相等,对应角相等的性质.


科目:初中数学 来源: 题型:解答题
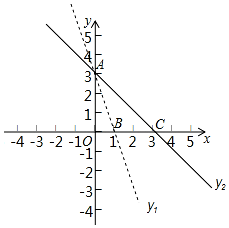 已知函数y1=k1x+b1和y2=k2x+b2图象如图所示,直线y1与直线y2交于A点(0,3).与x轴的交点坐标为B(1,0)、C(3,0).
已知函数y1=k1x+b1和y2=k2x+b2图象如图所示,直线y1与直线y2交于A点(0,3).与x轴的交点坐标为B(1,0)、C(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
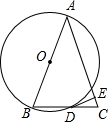 如图,△ABC的边AB为⊙O的直径,BC与⊙O交于点D,D为BC的中点,过点D作DE⊥AC于E.
如图,△ABC的边AB为⊙O的直径,BC与⊙O交于点D,D为BC的中点,过点D作DE⊥AC于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:二次函数y=x2-2x-3.
已知:二次函数y=x2-2x-3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
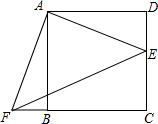 如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转至△ABF的位置.
如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转至△ABF的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
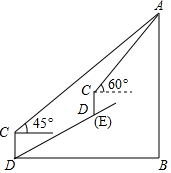 如图,在一次数学课外实践活动中,要求测量山坡前某建筑物的高度 AB.小刚在D处用高1.5m的测角仪CD,测得该建筑物顶端A的仰角为45°,然后沿倾斜角为30°的山坡向上前进20m到达E,重新安装好测角仪CD后又测得该建筑物顶端A的仰角为60°.求该建筑物的高度AB.(结果保留根号)
如图,在一次数学课外实践活动中,要求测量山坡前某建筑物的高度 AB.小刚在D处用高1.5m的测角仪CD,测得该建筑物顶端A的仰角为45°,然后沿倾斜角为30°的山坡向上前进20m到达E,重新安装好测角仪CD后又测得该建筑物顶端A的仰角为60°.求该建筑物的高度AB.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com