
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=8cm,则△BED的周长是__________.

8cm.
【考点】角平分线的性质;等腰直角三角形.
【分析】根据角平分线上的点到角的两边的距离相等可得CD=DE,再根据“HL”证明△ACD和△AED全等,根据全等三角形对应边相等可得AC=AE,然后求出△BED的周长=AB,即可得解.
【解答】解:∵∠C=90°,AD平分∠CAB,DE⊥AB,
∴CD=DE,
在△ACD和△AED中,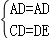 ,
,
∴△ACD≌△AED(HL),
∴AC=AE,
∴△BED的周长=DE+BD+BE,
=BD+CD+BE,
=BC+BE,
=AC+BE,
=AE+BE,
=AB,
∵AB=8cm,
∴△BED的周长是8cm.
故答案为:8cm.
【点评】本题考查了角平分线上的点到角的两边的距离相等的性质,全等三角形的判定与性质,熟记性质并求出△BED的周长=AB是解题的关键.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
为了估计鱼塘中鱼的条数,养鱼者首先从鱼塘中打捞30条鱼做上标记,然后放归鱼塘,经过一段时间,等有标记的鱼完全混合于鱼群中,再打捞200条鱼,发现其中带标记的鱼有5条,则鱼塘中估计有 条鱼.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知∠1=∠2,要得到△ABD≌△ACD,还需从下列条件中补选一个,则错误的选法是( )

A.AB=AC B.DB=DC C.∠ADB=∠ADC D.∠B=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
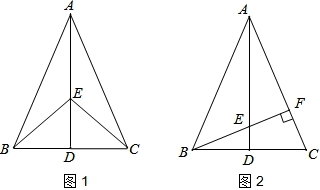
如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.
查看答案和解析>>
科目:初中数学 来源: 题型:
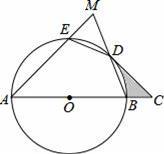
如图,AB是⊙O的直径,
 =
=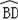
 ,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
(1)若OA=CD=2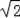
 ,求阴影部分的面积;
,求阴影部分的面积;
(2)求证:DE=DM.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com