
如图,已知∠1=∠2,要得到△ABD≌△ACD,还需从下列条件中补选一个,则错误的选法是( )

A.AB=AC B.DB=DC C.∠ADB=∠ADC D.∠B=∠C
B【考点】全等三角形的判定.
【分析】先要确定现有已知在图形上的位置,结合全等三角形的判定方法对选项逐一验证,排除错误的选项.本题中C、AB=AC与∠1=∠2、AD=AD组成了SSA是不能由此判定三角形全等的.
【解答】解:A、∵AB=AC,
∴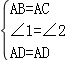 ,
,
∴△ABD≌△ACD(SAS);故此选项正确;
B、当DB=DC时,AD=AD,∠1=∠2,
此时两边对应相等,但不是夹角对应相等,故此选项错误;
C、∵∠ADB=∠ADC,
∴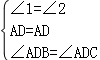 ,
,
∴△ABD≌△ACD(ASA);故此选项正确;
D、∵∠B=∠C,
∴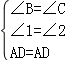 ,
,
∴△ABD≌△ACD(AAS);故此选项正确.
故选:B.
【点评】本题考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,但SSA无法证明三角形全等.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
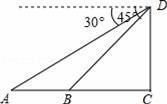
如图,为了测量河的宽度AB,测量人员在高21m的建筑物CD的顶端D处测得河岸B处的俯角为45°,测得河对岸A处的俯角为30°(A、B、C在同一条直线上),则河的宽度AB约是多少m?(精确到0.1m).(参考数据: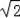
 ≈1.41,
≈1.41,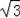
 ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
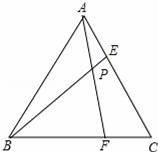
等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.
(1)若AE=CF;
①求证:AF=BE,并求∠APB的度数;
②若AE=2,试求AP•AF的值;
(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com