Question

【题目】猜想与证明：如图①摆放矩形纸片ABCD与矩形纸片ECGF，使B，C，G三点在一条直线上，CE在边CD上．连结AF，若M为AF的中点，连结DM，ME，试猜想DM与ME的数量关系，并证明你的结论．

拓展与延伸：

(1)若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF，其他条件不变，则DM和ME的关系为__________________；

(2)如图②摆放正方形纸片ABCD与正方形纸片ECGF，使点F在边CD上，点M仍为AF的中点，试证明(1)中的结论仍然成立．[提示：直角三角形斜边上的中线等于斜边的一半]

① 　②

Answer 1

【答案】猜想与证明：猜想DM与ME的数量关系是：DM＝ME，证明见解析；拓展与延伸：(1)DM＝ME，DM⊥ME；(2)证明见解析

【解析】

猜想：延长EM交AD于点H，利用△FME≌△AMH，得出HM=EM，再利用直角三角形中，斜边的中线等于斜边的一半证明．

（1）延长EM交AD于点H，利用△FME≌△AMH，得出HM=EM，再利用直角三角形中，斜边的中线等于斜边的一半证明，

（2）连接AC，AC和EC在同一条直线上，再利用直角三角形中，斜边的中线等于斜边的一半证明，

解：猜想与证明：

猜想DM与ME的数量关系是：DM＝ME.

证明：如图①，延长EM交AD于点H.

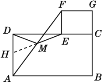①

∵四边形ABCD、四边形ECGF都是矩形，

∴AD∥BG，EF∥BG，∠HDE＝90°.

∴AD∥EF.

∴∠AHM＝∠FEM.

又∵AM＝FM，∠AMH＝∠FME，

∴△AMH≌△FME.

∴HM＝EM.

又∵∠HDE＝90°，

∴DM＝EH＝ME；

（1）∵四边形ABCD和CEFG是正方形，
∴AD∥EF，
∴∠EFM=∠HAM，
又∵∠FME=∠AMH，FM=AM，
在△FME和△AMH中，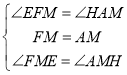
，

∴△FME≌△AMH（ASA）
∴HM=EM，
在RT△HDE中，HM=EM，
∴DM=HM=ME，
∴DM=ME．
∵四边形ABCD和CEFG是正方形，
∴AD=CD，CE=EF，
∵△FME≌△AMH，
∴EF=AH，
∴DH=DE，
∴△DEH是等腰直角三角形，
又∵MH=ME，

故答案为：DM＝ME，DM⊥ME；

（2）证明：如图②，连结AC.

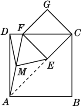②

∵四边形ABCD、四边形ECGF都是正方形，

∴∠DCA＝∠DCE＝∠CFE＝45°，

∴点E在AC上．

∴∠AEF＝∠FEC＝90°.

又∵点M是AF的中点，

∴ME＝AF.

∵∠ADC＝90°，点M是AF的中点，

∴DM＝AF.

∴DM＝ME.

∵ME＝AF＝FM，DM＝AF＝FM，

∴∠DFM＝ (180°－∠DMF)，∠MFE＝ (180°－∠FME)，

∴∠DFM＋∠MFE＝ (180°－∠DMF)＋ (180°－∠FME)

＝180°－ (∠DMF＋∠FME)

＝180°－∠DME.

∵∠DFM＋∠MFE＝180°－∠CFE＝180°－45°＝135°，

∴180°－∠DME＝135°.

∴∠DME＝90°.

∴DM⊥ME.