
【题目】观察下面三行数
①2,-4,8,-16,32,-64,......;
②4,-2,10,-14,34,-62,......;
③-1,2,-4,8,-16,32,......;
取每一行的第n个数,依次记为a,b,c. 如上图,当n=2时,x=-4,y=-2,z=2.
(1)当n=7时,请直接写出x、y、z的值,并求这三个数中最大的数与最小的数的差;
(2)已知n为偶数,且x、y、z这三个数中最大的数与最小的数的差为384,求n的值;
(3)若m=x+y+z,则x、y、z这三个数中最大的数与最小的数的差为______(用含m的式子表示)
【答案】(1)x=128,y=130,z=64,194;(2)n=8;(3)当n为奇数时差为![]() ;当n为偶数时差为
;当n为偶数时差为![]() .
.
【解析】
(1)根据已知发现:第①行的数,从第二个数开始,后面一个数是前面一个数乘2得到的,第②行的数第①行对应的数加2;第③行的数为第①行对应的数的一半的相反数,依此分别求出x、y、z的值,进而求解即可;
(2)首先判断出n为偶数时,z最大,x最小,再求出zx=![]() xx=
xx=![]() x,根据x、y、z这三个数中最大的数与最小的数的差为384列出方程,进而求出n的值;
x,根据x、y、z这三个数中最大的数与最小的数的差为384列出方程,进而求出n的值;
(3)根据m=x+y+z求出m=![]() ×(2)n+2,再分n为奇数与n为偶数两种情况讨论即可.
×(2)n+2,再分n为奇数与n为偶数两种情况讨论即可.
(1)根据题意,得x=(2)7=128,y=(2)7+2=130,z=![]() ×[(2)7]=64,
×[(2)7]=64,
这三个数中最大的数与最小的数的差为:130(64)=194;
(2)当n为偶数时,x<y<0,z>0,
∵z=![]() x,
x,
∴zx=![]() xx=
xx=![]() x=384,
x=384,
∴x=256,
∵(2)8=256,
∴n=8;
(3)m=x+y+z=(2)n+[(2)n+2]+{![]() ×[(2)n]}
×[(2)n]}
=(2)n(2)n+2-![]() ×[-(2)n]
×[-(2)n]
=![]() ×(2)n+2,
×(2)n+2,
①当n为奇数时,y>x>z,
yz=[(2)n+2]{ ![]() ×[(2)n]}
×[(2)n]}
=(2)n+2![]() ×(2)n
×(2)n
=![]() ×(2)n+2
×(2)n+2
=![]()
②当n为偶数时,z>y>x,
zx={![]() ×[(2)n]}[(2)n]
×[(2)n]}[(2)n]
=![]() ×(2)n
×(2)n
=![]() ×(2)n
×(2)n
=![]()
故答案为当n为奇数时差为![]() ;当n为偶数时差为
;当n为偶数时差为![]() .
.


科目:初中数学 来源: 题型:
【题目】(1)到目前为止,已研究的图形变换有哪几种?这些变换的共同性质有哪些?
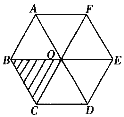
(2)如图,O是正六边形ABCDEF的中心,图中可由△OBC旋转得到的三角形有a个,可由△OBC平移得到的三角形有b个,可由△OBC轴对称得到的三角形有c个,试求(a+b+c)a+b-c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 图像与一次函数
图像与一次函数![]() 图像交于点A(1,4)和点B(m,--2).
图像交于点A(1,4)和点B(m,--2).

(1)求这两个函数的关系式;
(2)观察图像,写出使得![]() 成立的自变量x的取值范围;
成立的自变量x的取值范围;
(3)连结OA,OB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,搭一个正方形需要4根火柴棒,搭2个正方形需要7根火柴棒,搭3个正方形需要10根火柴棒.
![]() ……
……
(1)若搭5个这样的正方形,这需要 根火柴棒;
(2)若搭n个这样的正方形,这需要 根火柴棒;
(3)若现在有2018根火柴棒,要搭700个这样的正方形,至少还需要火柴多少根?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】猜想与证明:如图①摆放矩形纸片ABCD与矩形纸片ECGF,使B,C,G三点在一条直线上,CE在边CD上.连结AF,若M为AF的中点,连结DM,ME,试猜想DM与ME的数量关系,并证明你的结论.
拓展与延伸:
(1)若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为__________________;
(2)如图②摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.[提示:直角三角形斜边上的中线等于斜边的一半]
 ①
①  ②
②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题
已知张强家.体育场.文具店在同一直线上.下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.图中x表示时间,y表示张强离家的距离.据图象回答下列问题:
(1)体育场离张强家多远?张强从家到体育场用了多少时间?
(2)张强在文具店停留了多少时间?
(3)张强从文具店回家平均每分钟走多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某水库一周内水位高低的变化情况(用正数记水位比前一日上升数,用负数记下降数).那么本周星期几水位最低 ( )

A. 星期二B. 星期四C. 星期六D. 星期五
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求△MCB的面积S△MCB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a、b在数轴上的对应点如图所示
![]()
(1) 填空:(填“<”、“>”或“=”)
a_________0;b_________0;|a+b|_________|a|+|b|
(2) 用“<”将a、b、-b、![]() 、0连接起来
、0连接起来
(3) 化简:|a+b|-|b+1|-|a-1|=______________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com