【题目】计算：
（1）18-（-13）+（-27）-15 （2）（-23）+|-16|-|-7|-（-35）
（3）
（4）
（5） 
（6）
【答案】（1）-11；（2）21；（3）-1399；（4）
；（5）-
；（6）.
【解析】
（1）根据有理数加减法法则进行计算即可；
（2）先化简绝对值，然后再根据有理数加减法则进行计算即可；
（3）将
写成（
），除法变乘法，然后利用分配律进行计算即可；
（4）逆用乘法分配律进行计算即可；
（5）按顺序先进行乘方运算，乘除法运算，化简绝对值，然后再按运算顺序进行计算即可；
（6）先算乘方，再算乘除，最后计算加减即可.
（1）18-（-13）+（-27）-15
=18+13-27-15
=31-27-15
=-11；
（2）（-23）+|-16|-|-7|-（-35）
=-23+16-7+35
=-7-7+35
=21；
（3）
=（）×（-14）
=-1400+1
=-1399；
（4）
=
=
=；
（5） 
=-1-
+
=-1-1+
=-；
（6）
=-4×
-（-1）
=
=.
科目：初中数学 来源： 题型：
【题目】某自行车厂一周计划生产1400辆自行车，平均每天生产200辆，由于各种原因实际每天生产量与计划量相比有出入．下表是某周的生产情况（超产为正、减产为负）：
（1）根据记录可知前三天共生产______辆；
（2）产量最多的一天比产量最少的一天多生产______辆；
（3）该厂实行每周计件工资制，每生产一辆车可得60元，若超额完成任务，则超过部分每辆另奖15元；少生产一辆扣15元，那么该厂工人这一周的工资总额是多少？请说明理由.
（4）若将上面第（3）问中“实行每周计件工资制”改为“实行每日计件工资制”，其他条件不变，在此方式下该厂工人这一周按日计件工资与按周计件的工资哪一个更多？请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
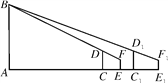
【题目】如图，学校的操场上有一旗杆AB，甲在操场上的C处竖立3 m高的竹竿CD；乙从C处退到E处恰好看到竹竿顶端D与旗杆顶端B重合，量得CE＝3 m，乙的眼睛到地面的距离FE＝1.5 m；丙在C1处竖立3 m高的竹竿C1D1，乙从E处后退6 m到E1处，恰好看到两根竹竿和旗杆重合，且竹竿顶端D1与旗杆顶端B也重合，量得C1E1＝4 m．求旗杆AB的高．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知反比例函数
图像与一次函数
图像交于点A（1，4）和点B（m，--2）．
（1）求这两个函数的关系式；
（2）观察图像，写出使得
成立的自变量x的取值范围；
（3）连结OA，OB，求△AOB的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在正方形ABCD中，点P是AB上一动点(不与A，B重合)，对角线AC，BD相交于点O，过点P分别作AC，BD的垂线，分别交AC，BD于点E，F，交AD，BC于点M，N.下列结论：①△APE≌△AME；②PM＋PN＝BD；③PE2＋PF2＝PO2.其中正确的有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如下图，搭一个正方形需要4根火柴棒，搭2个正方形需要7根火柴棒，搭3个正方形需要10根火柴棒．
……
(1)若搭5个这样的正方形，这需要 根火柴棒；
(2)若搭n个这样的正方形，这需要 根火柴棒；
(3)若现在有2018根火柴棒，要搭700个这样的正方形，至少还需要火柴多少根？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】猜想与证明：如图①摆放矩形纸片ABCD与矩形纸片ECGF，使B，C，G三点在一条直线上，CE在边CD上．连结AF，若M为AF的中点，连结DM，ME，试猜想DM与ME的数量关系，并证明你的结论．
拓展与延伸：
(1)若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF，其他条件不变，则DM和ME的关系为__________________；
(2)如图②摆放正方形纸片ABCD与正方形纸片ECGF，使点F在边CD上，点M仍为AF的中点，试证明(1)中的结论仍然成立．[提示：直角三角形斜边上的中线等于斜边的一半]
① 
②
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下表是某水库一周内水位高低的变化情况(用正数记水位比前一日上升数，用负数记下降数)．那么本周星期几水位最低 （ ）
A. 星期二B. 星期四C. 星期六D. 星期五
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：只有一组对角是直角的四边形叫做损矩形，连结它的两个非直角顶点的线段叫做这个损矩形的直径.
【1】如图1，损矩形ABCD，∠ABC=∠ADC=90°，则该损矩形的直径是线段 .
【1】在线段AC上确定一点P，使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上)，请作出这个圆，并说明你的理由. 友情提醒：“尺规作图”不要求写作法，但要保留作图痕迹．
【1】如图2，△ABC中，∠ABC＝90°，以AC为一边向形外作菱形ACEF，D为菱形ACEF的中心，连结BD，当BD平分∠ABC时，判断四边形ACEF为何种特殊的四边形？请说明理由. 若此时AB＝3，BD＝
，求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com