
【题目】一辆快车与一辆慢车分别从甲、乙两地同时出发,沿同一路线相向 而行,抵达对方出发地时停止运动.设慢车行驶xh时,两车之间的路程为ykm.图中折线ABCD表示y与x的函数关系,根据图像,解决以下问题:
(1)慢车的速度为多少km/h,快车的速度为多少km/h;
(2)解释图中点C的实际意义,求出点C的坐标;
(3)当x取何值时,y=500 ?
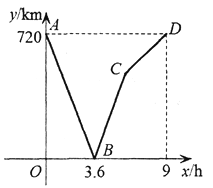
【答案】(1)80,120;(2)点C表示时间为6h快车到达乙地并停止运动,(6,480);(3)x=1.1或6.25.
【解析】
(1)由图象可知甲乙两地相距720km,慢车走完全程需要9h,即可求出慢车的速度,根据两车3.6h相遇,便可求也快车的速度;
(2)利用图象得出点C表示时间为6h,快车到达乙地并停止运动,此时点C坐标为(6,480);
(3)两车相遇之前和两车相遇之后都会出现y=500的情况,相遇之前500表示两车未走的路程,相遇之后500表示两车走过的路程,分别列方程解答即可.
解:(1)由图象可知甲乙两地相距720km,慢车走完全程需要9h,
慢车的速度为:720÷9=80(km/h),
由图象可知两车出发后3.6h相遇,则两车速度和为:720÷3.6=200km/h,
快车的速度为:200-80=120(km/h);
(2)点C的实际意义是:当时间为6h时,快车到达乙地并停止运动,
720÷120=6h,80×6=480km,
∴点C的坐标为(6,480);
(3)由图象可知,两车相遇时间3.6h,y=500时,有以下两种情况:
①两车相遇之前:120x+80x=720-500,解得x=1.1;
②两车相遇之后:由点C意义可知,快车到达乙地时,两车相遇480km,
∴500-480=80(x-6),解得x=6.25,
所以当x=1.1或6.25时,y=500.
故答案为:(1)80,120;(2)点C表示时间为6h快车到达乙地并停止运动,(6,480);(3)x=1.1或6.25.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地将一批物品匀速运往B地,已知甲出发0.5h后乙开始出发,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,请结合图中的信息解决如下问题: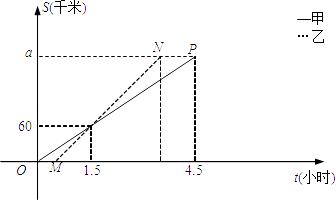
(1)计算甲、乙两车的速度及a的值;
(2)乙车到达B地后以原速立即返回.
①在图中画出乙车在返回过程中离A地的距离S(km)与时间t(h)的函数图象;
②请问甲车在离B地多远处与返程中的乙车相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠A=90°,点D是BC的中点,点E,F分别在AB,AC上,且∠EDF=90°,连接EF,求证:BE2+CF2=EF2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用如图所示的A,B两个转盘进行“配紫色”游戏(红色和蓝色在一起就配成了紫色,其中A盘中红色和蓝色均为半圆,B盘中红色、蓝色、绿色所在扇形圆心角均为120度).小亮和小刚同时用力转动两个转盘,当转盘停下时,两枚指针停留的区域颜色刚好配成紫色时小亮获胜,否则小刚获胜.判断这个游戏对双方是否公平,并借助树状图或列表说明理由.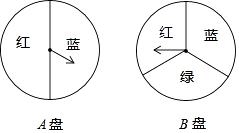
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A、点B的坐标分别为(4,0)、(0,3).
(1)求AB的长度.
(2)如图2,若以AB为边在第一象限内作正方形ABCD,求点C的坐标.

(3)在x轴上是否存一点P,使得⊿ABP是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发匀速前行,且途中休息一段时间后继续以原速前行.家到公园的距离为2000m,如图是小明和爸爸所走的路程S(m)与步行时间t(min)的函数图象.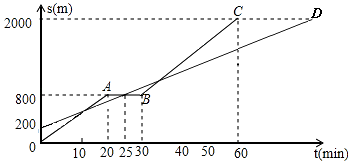
(1)直接写出BC段图象所对应的函数关系式(不用写出t的取值范围).
(2)小明出发多少时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早18分钟到达公园,则小明在步行过程中停留的时间需减少分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将两个边长为1的小正方形分别沿对角线剪开,拼成正方形ABCD.
(1)正方形ABCD的面积为 ,边长为 ,对角线BD= ;
(2)求证:![]() ;
;
(3)如图②,将正方形ABCD放在数轴上,使点B与原点O重合,边AB落在x轴的负半轴上,则点A所表示的数为 ,若点E所表示的数为整数,则点E所表示的数为 .


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )
A.当a=1时,函数图象过点(﹣1,1)
B.当a=﹣2时,函数图象与x轴没有交点
C.若a>0,则当x≥1时,y随x的增大而减小
D.不论a为何值,函数图象必经过(2,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【发现】:如图1,在正三角形ABC中,在AB,AC边上分别取点M,N,BM=AN,连接BN,CM,相交于点O,求∠α
易得:△ABN≌△BCN,则∠1=∠2
∵∠α是△BOC的外角,∴∠α=∠2+∠3
∴∠α=∠1+∠3=∠ABC=60°
【推广】:在正n边形中,对相邻的两边实施同样的操作…
(1)如图2,在正四边形ABCD中,在AB,AD边上分别取点M,N,连接BN,CM,可确定∠α=°;
(2)如图3,在正五边形ABCDE中,在AB,AD边上分别取点M,N,连接BN,CM,可确定∠α=°;
(3)判断:∠α可以等于160°吗?如果可以,求出对应的边数n,若不可以,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com