练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

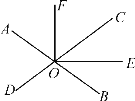
    【题目】如图，直线AB，CD相交于点O，OE是∠COB的平分线，∠FOE＝90°，若∠AOD＝70°.

    (1)求∠BOE的度数；

    (2)OF是∠AOC的平分线吗？请说明理由．

    【答案】（1）35°；（2）OF是∠AOC的平分线，理由见解析

    【解析】

    （1）根据角平分线的性质解答；

    （2）根据邻补角的性质、角平分线的定义解答．

    (1) 因为∠BOC和∠AOD是对顶角，所以∠BOC＝∠AOD＝70°，因为OE是∠COB的平分线，所以∠BOE＝∠BOC＝35°

    (2) OF是∠AOC的平分线，理由：因为∠AOD＝70°，∠COE＝∠BOE＝35°，所以∠AOC＝180°－70°＝110°，又∠FOC＝90°－∠COE＝55°，所以∠AOF＝∠AOC－∠FOC＝110°-55°＝55°，所以∠FOC＝∠AOF，即OF是∠AOC的平分线.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点A，C分别在x轴，y轴上，四边形ABCO为矩形，AB=16，AC=20,点D与点A关于y轴对称，点E、F分别是线段AD、AC上的动点（点E不与点A、D重合），且∠CEF=∠ACB.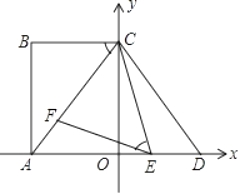

    （1）直接写出BC的长是 ， 点D的坐标是；
    （2）证明：△AEF与△DCE相似；
    （3）当△EFC为等腰三角形时，求点E的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)观察推理：如图 1，△ABC 中，∠ACB=90°，AC=BC,直线 L 过点C，点 A,B 在直线 L 同侧，BD⊥L， AE⊥L，垂足分别为D,E

    求证:△AEC≌△CDB

    （2）类比探究：如图 2，Rt△ABC 中，∠ACB=90°，AC=4，将斜边 AB 绕点 A 逆时针旋转 90°至 AB’, 连接B’C，求△AB’C 的面积

    （3）拓展提升：如图 3，等边△EBC 中，EC=BC=3cm，点 O 在 BC 上且 OC=2cm，动点 P 从点 E 沿射线EC 以 1cm/s 速度运动，连接 OP,将线段 OP 绕点O 逆时针旋转 120°得到线段 OF，设点 P 运动的时间为t 秒。

    当t= 秒时，OF∥ED

    若要使点F 恰好落在射线EB 上，求点P 运动的时间t

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，是抛物线y=ax2+bx+c（a≠0）图象的一部分，已知抛物线的对称轴为x=2，与x轴的一个交点是（﹣1，0）．下列结论： ①ac＜0；
    ②4a﹣2b+c＞0；
    ③抛物线与x轴的另一个交点是（4，0）；
    ④点（﹣3，y1），（6，y2）都在抛物线上，则有y1＜y2 ． 其中正确的个数为（ ）

    A.1
    B.2
    C.3
    D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点P是∠AOB的边OB上的一点，过点P画OB的垂线，交OA于点C；

    （1） 过点C画OB的平行线CD；

    （2） 过点P画OA的垂线，垂足为H；

    （3） 线段PH的长度是点P到 的距离，线段 的长度是点C到直线OB的距离．线段PC、PH、OC这三条线段大小关系是 （用“＜”号连接）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学校准备购置甲乙两种羽毛球拍若干，已知甲种球拍的单价比乙种球拍的单价多40元，且购买4副甲种球拍与购买6副乙种球拍的费用相同．
    （1）两种球拍的单价各是多少元？
    （2）若学校准备购买100副甲乙两种羽毛球拍，且购买甲种球拍的费用不少于乙种球拍费用的3倍，问购买多少副甲种球拍总费用最低？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在学习解直角三角形以后，重庆八中数学兴趣小组测量了旗杆的高度．如图，某一时刻，旗杆AB的影子一部分落在平台上的影长BC为6米，落在斜坡上的影长CD为4米，AB⊥BC，同一时刻，光线与旗杆的夹角为37°，斜坡的坡角为30°，旗杆的高度AB约为（ ）米．（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75， ≈1.73）

    A.10.61
    B.10.52
    C.9.87
    D.9.37

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某工程队修建一条长1200 m的道路，采用新的施工方式，工效提升了50%，结果提前4天完成任务.

    （1）求这个工程队原计划每天修道路多少米？

    （2）在这项工程中，如果要求工程队提前2天完成任务，那么实际平均每天修建道路的工效比原计划增加百分之几？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=﹣ x2﹣ x+ 与x轴交于A，B两点（A点在B点的左侧），与y轴交于点C，已知点D（0，﹣ ）．

    （1）求直线AC的解析式；
    （2）如图1，P为直线AC上方抛物线上的一动点，当△PBD面积最大时，过P作PQ⊥x轴于点Q，M为抛物线对称轴上的一动点，过M作y轴的垂线，垂足为点N，连接PM，NQ，求PM+MN+NQ的最小值；
    （3）在（2）问的条件下，将得到的△PBQ沿PB翻折得到△PBQ′，将△BPQ′沿直线BD平移，记平移中的△PBQ′为△P′B′Q″，在平移过程中，设直线P′B′与x轴交于点E．则是否存在这样的点E，使得△B′EQ″为等腰三角形？若存在，求此时OE的长．

    查看答案和解析>>

    同步练习册答案