
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),点P是x轴上一动点,过点P作x轴的垂线交抛物线于点C,交直线AB于点D,设P(x,0).

(1)求抛物线的函数表达式;
(2)当0<x<3时,求线段CD的最大值;
(3)在△PDB和△CDB中,当其中一个三角形的面积是另一个三角形面积的2倍时,求相应x的值;
(4)过点B,C,P的外接圆恰好经过点A时,x的值为 .(直接写出答案)
【答案】(1) y=﹣x2+2x+3;(2) ![]() ;(3)x=±
;(3)x=±![]() 或x=±2;(4)x=±
或x=±2;(4)x=±![]() .
.
【解析】分析:(1)用待定系数法求出抛物线解析式即可;(2)先确定出直线AB解析式,进而得出点D,C的坐标,即可得出CD的函数关系式,即可得出结论;(3)先确定出CD=|-x2+3x|,DP=|-x+3|,再分两种情况解绝对值方程即可;
(4)利用四个点在同一个圆上,得出过点B,C,P的外接圆的圆心既是线段AB的垂直平分线上,也在线段PC的垂直平分线上,建立方程即可.
本题解析:
(1)∵抛物线y=﹣x2+bx+c与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),∴﹣9+3b+c=0,c=3,∴b=2,∴抛物线解析式为y=﹣x2+2x+3;
(2)∵A(3,0),B(0,3),∴直线AB解析式为y=﹣x+3,
∵P(x,0).∴D(x,﹣x+3),C(x,﹣x2+2x+3),
∵0<x<3,∴CD=﹣x2+2x+3﹣(﹣x+3)=﹣x2+3x=﹣(x﹣![]() )2+
)2+![]() ,当x=
,当x=![]() 时,CD最大=
时,CD最大=![]() ;
;
(3)由(2)知,CD=|﹣x2+3x|,DP=|﹣x+3|
①当S△PDB=2S△CDB时,∴PD=2CD,即:2|﹣x2+3x|=|﹣x+3|,∴x=±![]() 或x=3(舍),
或x=3(舍),
②当2S△PDB=S△CDB时,∴2PD=CD,即:|﹣x2+3x|=2|﹣x+3|,∴x=±2或x=3(舍),
即:综上所述,x=±![]() 或x=±2;
或x=±2;
(4)直线AB解析式为y=﹣x+3,∴线段AB的垂直平分线l的解析式为y=x,
∵过点B,C,P的外接圆恰好经过点A,
∴过点B,C,P的外接圆的圆心既是线段AB的垂直平分线上,也在线段PC的垂直平分线上,
∴![]() ,∴x=±
,∴x=±![]() ,故答案为:
,故答案为: ![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图①,已知⊙O的半径为1,PQ是⊙O的直径,n个相同的正三角形沿PQ排成一列,所有正三角形都关于PQ对称,其中第一个△A1B1C1的顶点A1与点P重合,第二个△A2B2C2的顶点A2是B1C1与PQ的交点……最后一个△AnBnCn的顶点Bn,Cn在圆上.



(1)如图②,当n=1时,求正三角形的边长a1.
(2)如图③,当n=2时,求正三角形的边长a2.
(3)如图①,求正三角形的边长an(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
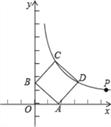
【题目】如图,点P(![]() +1,
+1, ![]() ﹣1)在双曲线y=kx-1(x>0)上.
﹣1)在双曲线y=kx-1(x>0)上.
(1)求k的值;
(2)若正方形ABCD的顶点C,D在双曲线y=kx-1(x>0)上,顶点A,B分别在x轴和y轴的正半轴上,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是( ) 
A.y=2x+3
B.y=x﹣3
C.y=2x﹣3
D.y=﹣x+3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com