
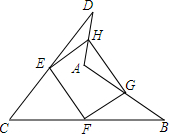
 如图所示,点E,F,G,H分别是CD,BC,AB,DA的中点,求证:四边形EFGH是平行四边形.
如图所示,点E,F,G,H分别是CD,BC,AB,DA的中点,求证:四边形EFGH是平行四边形. 分析 证明EF是△BCD的中位线,GH是△ABD的中位线,由三角形中位线定理得出EF∥BD,EF=$\frac{1}{2}$BD,GH∥BD,GH=$\frac{1}{2}$BD,得出EF∥GH,EF=GH,即可得出结论.
解答 证明:连接BD.如图所示: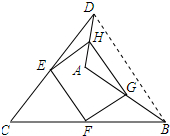
∵点E,F,G,H分别是CD,BC,AB,DA的中点,
∴EF是△BCD的中位线,GH是△ABD的中位线,
∴EF∥BD,EF=$\frac{1}{2}$BD,GH∥BD,GH=$\frac{1}{2}$BD,
∴EF∥GH,EF=GH,
∴四边形EFGH是平行四边形.
点评 本题考查了平行四边形的判定方法、三角形中位线定理;熟练掌握平行四边形的判定方法,证明三角形中位线是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 知图,有一块长80cm,宽60cm的长方形硬纸片,在四角各剪去一个同样的小正方形,用剩余部分做成一个底面积为1500cm2的无盖的长方体盒子,求剪去的小正方形的边长.
知图,有一块长80cm,宽60cm的长方形硬纸片,在四角各剪去一个同样的小正方形,用剩余部分做成一个底面积为1500cm2的无盖的长方体盒子,求剪去的小正方形的边长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com