
【题目】AB⊥BC,∠1+∠2=90°,∠2=∠3.BE与DF平行吗?为什么?
(解析)解:BE∥DF.
∵AB⊥BC,
∴∠ABC= °,
即∠3+∠4= °.
又∵∠1+∠2=90°,
且∠2=∠3,
∴ = .
理由是: .
∴BE∥DF.
理由是: .

科目:初中数学 来源: 题型:
【题目】某汽车制造厂开发一款新式电动汽车,计划一年生产安装![]() 辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人.他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:
辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人.他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:![]() 名熟练工和
名熟练工和![]() 名新工人每月可安装
名新工人每月可安装![]() 辆电动汽车;
辆电动汽车;![]() 名熟练工和
名熟练工和![]() 名新工人每月可安装
名新工人每月可安装![]() 辆电动汽车.
辆电动汽车.
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘![]() 名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在△ABC中,∠A![]() ,P是BC边上的一点,
,P是BC边上的一点,![]() ,
,![]() 是点P关于AB、AC的对称点,连结
是点P关于AB、AC的对称点,连结![]() ,分别交AB、AC于点D、E.
,分别交AB、AC于点D、E.
①若![]() ,求
,求![]() 的度数;
的度数;
②请直接写出∠A与![]() 的数量关系:___________________________;
的数量关系:___________________________;
(2)如图2,在△ABC中,若∠BAC![]() ,用三角板作出点P关于AB、AC的对称点
,用三角板作出点P关于AB、AC的对称点![]() 、
、![]() ,(不写作法,保留作图痕迹),试判断点
,(不写作法,保留作图痕迹),试判断点![]() ,
,![]() 与点A是否在同一直线上,并说明理由.
与点A是否在同一直线上,并说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=ax2+bx+c过点A(﹣1,0),且经过直线y=x﹣3与坐标轴的两个交点B、C.
(1)求抛物线的表达式;
(2)若点M在第四象限内且在抛物线上,有OM⊥BC,垂足为D,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(1,2),B(3,1),C(﹣2,﹣1).

(1)在图中作出△ABC关于x轴的对称图形△A1B1C1 ;
(2)写出点A1 , B1 , C1的坐标(直接写答案), A1________ ,B1________ ,C1________;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,若抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B也在抛物线L1上(点A与点B不重合),我们定义:这样的两条抛物L1,L2互为“友好”抛物线,可见一条抛物线的“友好”抛物线可以有多条.
(1)如图2,已知抛物线L3:y=2x2-8x+4与y轴交于点C,试求出点C关于该抛物线对称轴对称的点D的坐标;
(2)请求出以点D为顶点的L3的友好抛物线L4的解析式,并指出L3与L4中y同时随x增大而增大的自变量的取值范围;
(3)若抛物y=a1 (x-m) 2+n的任意一条友好抛物线的解析式为y=a2 (x-h) 2+k,请写出a1与a2的关系式,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,将BC沿BD所在的直线折叠,使点C落在AB边上的E点处.
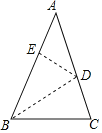
(1)若∠ADE=30°,求∠BDC的度数.
(2)若AB=AC=8,BC=5,求三角形AED的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com