
ЁОЬтФПЁПРіНВМХЉСхЃЌЪЧвЛжжМЋИЛЬиЩЋЕФЁЂаЮзДЭЌТэАяЕФТэСхЕФЙвМў.етжжТэАяЮФЛЏЩЬЦЗЃЌЪЧДПЪжЙЄжЦзї.ОЋжТаЁЧЩЕФЧрЭСхюѕЯТЯЕгавЛПщдВаЮФОПщЃЌЪжЛцзХИїжжИїбљЕФЛ.ФГЩЬЕъашвЊЙКНјМзЁЂввСНжжВМХЉСхЙВ300МўЃЌвЛМўМзжжВМХЉСхНјМлЮЊ340дЊЃЌЪлМлЮЊ400дЊЃЌвЛМўввжжВМХЉСхНјМлЮЊ380дЊЃЌЪлМлЮЊ460дЊ.ЃЈзЂЃКРћШѓ=ЪлМл-НјМлЃЉ
ЃЈ1ЃЉШєЩЬЕъМЦЛЎЯњЪлЭъетХњВМХЉСхКѓФмЛёРћ21600дЊЃЌЮЪМзЁЂввСНжжВМХЉСхгІЗжБ№ЙКНјЖрЩйМўЃП
ЃЈ2ЃЉШєЩЬЕъМЦЛЎЭЖШызЪН№110000дЊЃЌдђФмЙКНјМзжжВМХЉСхЖрЩйМўЃП
ЁОД№АИЁПЃЈ1ЃЉЙКНјМзжжВМХЉСх120МўЃЌввжжВМХЉСх180МўЃЛЃЈ2ЃЉЙКНјМзжжВМХЉСх100Мў.
ЁОНтЮіЁП
ЃЈ1ЃЉЩшЙКНјМзжжВМХЉСхxМўЃЌввжжВМХЉСхyМўЃЌШЛКѓНјвЛВНСаГіЗНГЬзщЧѓНтМДПЩЃЛ
ЃЈ2ЃЉЩшЙКНјМзжжВМХЉСхaМўЃЌдђЙКНјввжжВМХЉСх![]() МўЃЌШЛКѓНјвЛВНСаГіЗНГЬЧѓНтМДПЩ.
МўЃЌШЛКѓНјвЛВНСаГіЗНГЬЧѓНтМДПЩ.
ЃЈ1ЃЉЩшЙКНјМзжжВМХЉСхxМўЃЌввжжВМХЉСхyМўЃЌ
дђ![]()
НтЕУ![]()
Д№ЃКЙКНјМзжжВМХЉСх120МўЃЌввжжВМХЉСх180МўЃЛ
ЃЈ2ЃЉЩшЙКНјМзжжВМХЉСхaМўЃЌдђЙКНјввжжВМХЉСх![]() МўЃЌ
МўЃЌ
ИљОнЬтвтЕУЃЌ![]()
НтЕУ![]() ЃЌ
ЃЌ
Д№ЃКЙКНјМзжжВМХЉСх100Мў.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
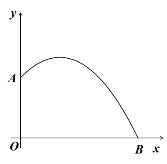
ЁОЬтФПЁПФГЙуГЁгавЛИіаЁаЭХчШЊЃЌЫЎСїДгДЙжБгкЕиУцЕФЫЎЙмOAХчГіЃЌOAГЄЮЊ1.5Уз.ЫЎСїдкИїИіЗНЯђЩЯбиаЮзДЯрЭЌЕФХзЮяЯпТЗОЖТфЕНЕиУцЩЯЃЌФГЗНЯђЩЯХзЮяЯпТЗОЖЕФаЮзДШчЭМЫљЪОЃЌТфЕуBЕНOЕФОрРыЮЊ3УзЃЎНЈСЂЦНУцжБНЧзјБъЯЕЃЌЫЎСїХчГіЕФИпЖШyЃЈУзЃЉгыЫЎЦНОрРыxЃЈУзЃЉжЎМфНќЫЦТњзуКЏЪ§ЙиЯЕ![]()
ЃЈ1ЃЉЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЧѓЫЎСїХчГіЕФзюДѓИпЖШЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪГЦЗСуЪлЕъЮЊЪГЦЗГЇДњЯњвЛжжУцАќЃЌЮДЪлГіЕФУцАќПЩвдЭЫЛиГЇМвЃЎОЭГМЦЯњЪлЧщПіЗЂЯжЃЌЕБетжжУцАќЕФЯњЪлЕЅМлЮЊ7НЧЪБЃЌУПЬьТєГі160ИіЃЎдкДЫЛљДЁЩЯЃЎЕЅМлУПЬсИп1НЧЪБЃЌИУСуЪлЕъУПЬьОЭЛсЩйТєГі20ИіУцАќЃЎЩшетжжУцАќЕФЯњЪлЕЅМлЮЊxНЧ(УПИіУцАќЕФГЩБОЪЧ5НЧ)ЃЎСуЪлЕъУПЬьЯњЪлетжжУцАќЕФРћШѓЮЊyНЧЃЎ
(1)гУКЌxЕФДњЪ§ЪНЗжБ№БэЪОГіУПИіУцАќЕФРћШѓгыТєГіЕФУцАќИіЪ§ЃЛ
(2)ЧѓxгыyжЎМфЕФКЏЪ§ЙиЯЕЪНЃК
(3)ЕБетжжУцАќЕФЯњЪлЕЅМлЖЈЮЊЖрЩйЪБЃЌИУСуЪлЕъУПЬьЯњЪлетжжУцАќЛёЕУЕФРћШѓзюДѓЃПзюДѓРћШѓЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌ![]() ЮЊзјБъдЕуЃЌЕу
ЮЊзјБъдЕуЃЌЕу![]() ЃЌЕу
ЃЌЕу![]() .
.
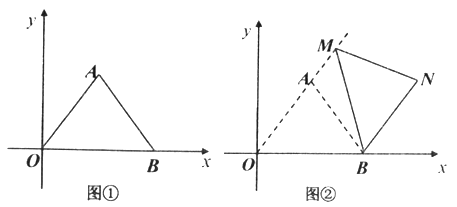
ЃЈЂёЃЉШчЭМЂйЃЌЧѓABЕФГЄЃЛ
ЃЈЂђЃЉШчЭМЂкЃЌАбЭМЂйжаЕФ![]() ШЦЕуBЫГЪБеыа§зЊЃЌЪЙЕуOЕФЖдгІЕуAMЧЁКУТфдкOAбгГЄЯпЩЯЃЌNЪЧЕуAа§зЊКѓЕФЖдгІЕу.
ШЦЕуBЫГЪБеыа§зЊЃЌЪЙЕуOЕФЖдгІЕуAMЧЁКУТфдкOAбгГЄЯпЩЯЃЌNЪЧЕуAа§зЊКѓЕФЖдгІЕу.
ЂйЧѓжЄЃК![]() ЃЛЂкЧѓЕуNЕФзјБъЃЛ
ЃЛЂкЧѓЕуNЕФзјБъЃЛ
ЃЈЂѓЃЉЕуCЪЧOBЕФжаЕуЃЌЕуDЮЊЯпЖЮOAЩЯЕФЖЏЕуЃЌдк![]() ШЦЕуBЫГЪБеыа§зЊЙ§ГЬжаЃЌЕуDЕФЖдгІЕуЪЧPЃЌЧѓЯпЖЮCPГЄЕФШЁжЕЗЖЮЇЃЈжБНгаДГіНсЙћЃЉ.
ШЦЕуBЫГЪБеыа§зЊЙ§ГЬжаЃЌЕуDЕФЖдгІЕуЪЧPЃЌЧѓЯпЖЮCPГЄЕФШЁжЕЗЖЮЇЃЈжБНгаДГіНсЙћЃЉ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЕъЯњЪл10ЬЈAаЭКЭ20ЬЈBаЭЕчФдЕФРћШѓЮЊ4000дЊЃЌЯњЪл20ЬЈAаЭКЭ10ЬЈBаЭЕчФдЕФРћШѓЮЊ3500дЊЃЎ
ЃЈ1ЃЉЧѓУПЬЈAаЭЕчФдКЭBаЭЕчФдЕФЯњЪлРћШѓЃЛ
ЃЈ2ЃЉИУЩЬЕъМЦЛЎвЛДЮЙКНјСНжжаЭКХЕФЕчФдЙВ100ЬЈЃЌЦфжаBаЭЕчФдЕФНјЛѕСПВЛГЌЙ§AаЭЕчФдЕФ2БЖЃЌЩшЙКНјAаЭЕчФдxЬЈЃЌет100ЬЈЕчФдЕФЯњЪлзмРћШѓЮЊyдЊЃЎ
ЂйЧѓyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЂкИУЩЬЕъЙКНјAаЭЁЂBаЭЕчФдИїЖрЩйЬЈЃЌВХФмЪЙЯњЪлзмРћШѓзюДѓЃП
ЃЈ3ЃЉЪЕМЪНјЛѕЪБЃЌГЇМвЖдAаЭЕчФдГіГЇМлЯТЕїmЃЈ0ЃМmЃМ100ЃЉдЊЃЌЧвЯоЖЈЩЬЕъзюЖрЙКНјAаЭЕчФд70ЬЈЃЌШєЩЬЕъБЃГжЭЌжжЕчФдЕФЪлМлВЛБфЃЌЧыФуИљОнвдЩЯаХЯЂМАЃЈ2ЃЉжаЬѕМўЃЌЩшМЦГіЪЙет100ЬЈЕчФдЯњЪлзмРћШѓзюДѓЕФНјЛѕЗНАИЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
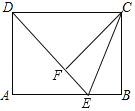
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌABЃН4ЃЌADЃН3ЃЌEЪЧБпABЩЯвЛЕуЃЌНЋЁїCBEбижБЯпCEЖделЃЌЕУЕНЁїCFEЃЌСЌНгDFЃЎ
ЃЈ1ЃЉЕБDЁЂEЁЂFШ§ЕуЙВЯпЪБЃЌжЄУїЃКDEЃНCDЃЛ
ЃЈ2ЃЉЕБBEЃН1ЪБЃЌЧѓЁїCDFЕФУцЛ§ЃЛ
ЃЈ3ЃЉШєЩфЯпDFНЛЯпЖЮABгкЕуPЃЌЧѓBPЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§yЃНxЉ1ЕФЭМЯѓгыxжсЃЌyжсЗжБ№НЛгкЕуAЃЌBЃЌгыЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓНЛгкЕуCЃЌDЃЌCEЁЭxжсгкЕуEЃЌ
ЕФЭМЯѓНЛгкЕуCЃЌDЃЌCEЁЭxжсгкЕуEЃЌ![]() ЃЎ
ЃЎ
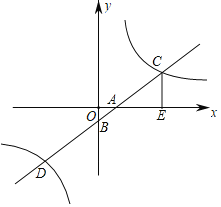
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФБэДяЪНгыЕуDЕФзјБъЃЛ
ЃЈ2ЃЉвдCEЮЊБпзїECMNЃЌЕуMдквЛДЮКЏЪ§yЃНxЉ1ЕФЭМЯѓЩЯЃЌЩшЕуMЕФКсзјБъЮЊaЃЌЕББпMNгыЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓгаЙЋЙВЕуЪБЃЌЧѓaЕФШЁжЕЗЖЮЇЃЎ
ЕФЭМЯѓгаЙЋЙВЕуЪБЃЌЧѓaЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈБОЬтТњЗж10ЗжЃЉ
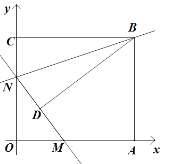
ШчЭМЃЌОиаЮAOCBЕФЖЅЕуAЁЂCЗжБ№ЮЛгкxжсКЭyжсЕФе§АыжсЩЯЃЌЯпЖЮOAЁЂOCЕФГЄЖШТњзуЗНГЬ|x-15|+=0(OBЃОOC)ЃЌжБЯпy=kx+bЗжБ№гыxжсЁЂyжсНЛгкMЁЂNСНЕуЃЌСЌНгBNЃЎНЋЁїBCNбижБЯпBNелЕўЃЌЕуCЧЁКУТфдкжБЯпMNЩЯЕФЕуDДІЃЌЧвtanЁЯCBD=.
ЂХ ЧѓЕуBЕФзјБъЃЎ
ЂЦ ЧѓжБЯпBNЕФНтЮіЪНЃЎ
ЂЧ НЋжБЯпBNвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШбиyжсЯђЯТЦНвЦЃЌЧѓжБЯпBNЩЈЙ§ОиаЮAOCBЕФУцЛ§SЙигкдЫЖЏЕФЪБМфtЃЈ0ЃМtЁм13ЃЉЕФКЏЪ§ЙиЯЕЪН.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
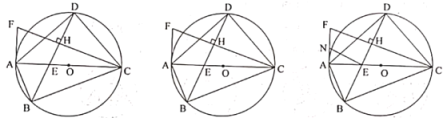
ЁОЬтФПЁПвбжЊЫФБпаЮ![]() ЮЊ
ЮЊ![]() ЕФФкНгЫФБпаЮЃЌжБОЖ
ЕФФкНгЫФБпаЮЃЌжБОЖ![]() гыЖдНЧЯп
гыЖдНЧЯп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌзї
ЃЌзї![]() гк
гк![]() ЃЌ
ЃЌ![]() гыЙ§
гыЙ§![]() ЕуЕФжБЯпЯрНЛгкЕу
ЕуЕФжБЯпЯрНЛгкЕу![]() ЃЌ
ЃЌ![]() .
.
ЃЈ1ЃЉЧѓжЄЃК![]() ЮЊ
ЮЊ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉШє![]() ЦНЗж
ЦНЗж![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЕФАыОЖЮЊ
ЕФАыОЖЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄ.
ЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com