
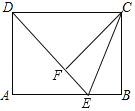
【题目】如图,矩形ABCD中,AB=4,AD=3,E是边AB上一点,将△CBE沿直线CE对折,得到△CFE,连接DF.
(1)当D、E、F三点共线时,证明:DE=CD;
(2)当BE=1时,求△CDF的面积;
(3)若射线DF交线段AB于点P,求BP的最大值.
【答案】(1)见解析;(2)![]() ;(3)4﹣
;(3)4﹣![]()
【解析】
(1)由矩形和折叠的性质可得∠DCE=∠CEB=∠FEC,即可证DE=CD;
(2)延长EF交CD的延长线于点G,由矩形和折叠的性质可证GE=GC,由勾股定理可求CG=5,即可求△CDF的面积;
(3)过点C作CH⊥DP于点H,连接CP,由相似三角形的性质可得![]() =
=![]() ,即当点H与点F重合时,CH最大,DH最小,AP最小,BP最大,由勾股定理可求AP的长,即可求BP的最大值.
,即当点H与点F重合时,CH最大,DH最小,AP最小,BP最大,由勾股定理可求AP的长,即可求BP的最大值.
证明:(1)∵四边形ABCD是矩形
∴AB=CD=4,AD=BC=3,AB∥CD,
∴∠DCE=∠CEB
∵△CBE翻折得到△CFE
∴∠FEC=∠CEB
∴∠DCE=∠FEC
∴DE=CD
(2)如图1,延长EF交CD的延长线于点G,
∵四边形ABCD是矩形
∴AB=CD=4,AD=BC=3,AB∥CD,
∴∠DCE=∠CEB
∵△CBE翻折得到△CFE
∴∠FEC=CEB,CF=BC=3,EF=BE=1,∠CFE=90°
∴∠DCE=∠FEC,∠CFG=90°
∴CG=EG,
∴GF=GE﹣EF=CG﹣1
∵在Rt△CGF中,CG2=CF2+GF2,
∴CG2=9+(CG﹣1)2,
解得:CG=5
∵△CDF与△CGF分别以CD、CG为底时,高相等
∴![]()
∴S△CDF=![]() S△CGF=
S△CGF=![]() =
=![]()
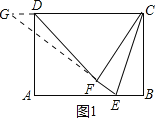
(3)如图2,过点C作CH⊥DP于点H,连接CP,
∵CD∥AB
∴∠CDP=∠APD,且∠A=∠CHD=90°
∴△ADP∽△HCD
∴![]() =
=![]() ,
,
∵CH≤CF,CF=BC=AD=3
∴CH≤3
∴当点H与点F重合时,
CH最大,DH最小,AP最小,BP最大,
此时,在△ADP与△HCD
∴△ADP≌△HCD(AAS)
∴CD=DP=4,AP=DF
∵AP=![]() =
=![]()
∴BP的最大值为4﹣![]() .
.



科目:初中数学 来源: 题型:
【题目】清朝数学家梅文鼎的著作《方程论》中有这样一道题:山田三亩,场地六亩,共折实田四亩七分;又山田五亩,场地三亩,共折实田五亩五分,问每亩山田折实田多少,
每亩场地折实田多少?
译文为:假如有山田3亩,场地6亩,其产粮相当于实田4.7亩;又山田5亩,场地3亩,其产粮相当于实田5.5亩,问每亩山田和每亩场地产粮各相当于实田多少亩?请你解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在△ABC和△EDC中,AC=CE=CB=CD,∠ACB=∠ECD=![]() ,AB与CE交于F,ED与AB、BC分别交于M、H.
,AB与CE交于F,ED与AB、BC分别交于M、H.
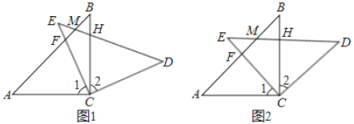
(1)求证:CF=CH;
(2)如图(2),△ABC不动,将△EDC绕点C旋转到∠BCE=![]() 时,试判断四边形ACDM是什么四边形?并证明你的结论.
时,试判断四边形ACDM是什么四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丽江布农铃,是一种极富特色的、形状同马帮的马铃的挂件.这种马帮文化商品,是纯手工制作.精致小巧的青铜铃铛下系有一块圆形木块,手绘着各种各样的画.某商店需要购进甲、乙两种布农铃共300件,一件甲种布农铃进价为340元,售价为400元,一件乙种布农铃进价为380元,售价为460元.(注:利润=售价-进价)
(1)若商店计划销售完这批布农铃后能获利21600元,问甲、乙两种布农铃应分别购进多少件?
(2)若商店计划投入资金110000元,则能购进甲种布农铃多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任大叔决定在承包的荒山上种樱桃树,第一次用1000元购进了一批树苗,第二次又用1000元购进该种树苗,但这次每棵树苗的进价是第一次进价的2倍,购进数量比第次少了100棵;
(1)求第一次每棵树苗的进价是多少元?
(2)一年后,树苗的成活率为85%,每棵樱桃树平均产樱桃30斤,任大叔将两批樱桃树所产樱桃按同一价格全部销售完毕后,获利不低于89800元,求每斤樱桃的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)
与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象相交于点A(1,4)和B(﹣2,n).
的图象与一次函数y2=ax+b的图象相交于点A(1,4)和B(﹣2,n).

(1)求反比例函数与一次函数的解析式;
(2)请根据图象直接写出y1<y2时,x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com