
【题目】如图(1),在△ABC和△EDC中,AC=CE=CB=CD,∠ACB=∠ECD=![]() ,AB与CE交于F,ED与AB、BC分别交于M、H.
,AB与CE交于F,ED与AB、BC分别交于M、H.
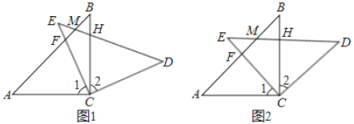
(1)求证:CF=CH;
(2)如图(2),△ABC不动,将△EDC绕点C旋转到∠BCE=![]() 时,试判断四边形ACDM是什么四边形?并证明你的结论.
时,试判断四边形ACDM是什么四边形?并证明你的结论.
【答案】(1)见解析;(2)菱形,理由见解析
【解析】
(1)要证明CF=CH,可先证明△BCF≌△ECH,由∠ABC=∠DCE=90°,AC=CE=CB=CD,可得∠B=∠E=45°,得出CF=CH;
(2)当旋转角∠BCD=45°,推出四边形ACDM是平行四边形,由AC=CD判断出四边形ACDM是菱形.
(1)∵AC=CE=CB=CD,∠ACB=∠ECD=90°,
∴∠A=∠B=∠D=∠E=45°,
在△BCF和△ECH中,
∵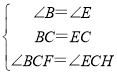 ,
,
∴△BCF≌△ECH(ASA),
∴CF=CH;
(2)∠BCE=45°时,四边形ACDM是菱形,
理由如下:
∵∠ACB=∠DCE=90°,∠BCE=45°,
∴∠ACE=∠DCB=45°.
∵∠E=45°,
∴∠ACE =∠E,
∴AC∥DE,
∴∠AMH=180°-∠A=135°,
又∵∠A=∠D=45°,
∴∠AMH+∠D=135°+45°=180![]() ,
,
∴AM∥CD,
∴四边形ACDM是平行四边形;
∵AC=CD,
∴四边形ACDM是菱形.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=ax+b与x轴交于点A(4,0),与y轴交于点B(0,﹣2),与反比例函数y=![]() (x>0)的图象交于点C(6,m).
(x>0)的图象交于点C(6,m).
(1)求直线和反比例函数的表达式;
(2)连接OC,在x轴上找一点P,使△OPC是以OC为腰的等腰三角形,请求出点P的坐标;
(3)结合图象,请直接写出不等式![]() ≥ax+b的解集.
≥ax+b的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在硬地上抛掷1枚图钉,通常会出现如图两种情况:

八(1)班张老师让同学们做抛掷图钉试验,每人抛掷1枚图钉20次,班长小明分別汇总5人、10人、15人…的试验结果,并将获得的数据填入下表:
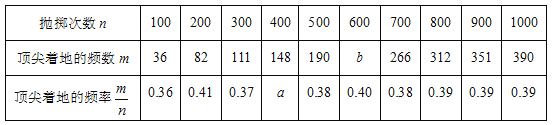
(1)填空:a= ,b= ;
(2)补全小明根据试验数据绘制的折线统计图;
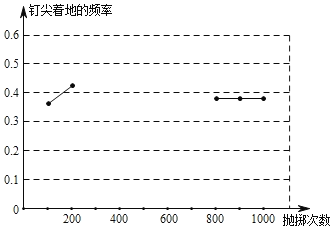
(3)仔细观察“抛掷图钉试验”的数据统计表和统计图,试估计“钉尖不着地”的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品现在的售价为每件60元,每星期可卖出300件. 市场调查反映:如调整价格,每降价1元,每星期可多卖出20件. 已知商品的进价为每件40元,如何定价才能使利润最大?这个最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品零售店为食品厂代销一种面包,未售出的面包可以退回厂家.经统计销售情况发现,当这种面包的销售单价为7角时,每天卖出160个.在此基础上.单价每提高1角时,该零售店每天就会少卖出20个面包.设这种面包的销售单价为x角(每个面包的成本是5角).零售店每天销售这种面包的利润为y角.
(1)用含x的代数式分别表示出每个面包的利润与卖出的面包个数;
(2)求x与y之间的函数关系式:
(3)当这种面包的销售单价定为多少时,该零售店每天销售这种面包获得的利润最大?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=65°,以点A为旋转中心,将△ABC绕点A逆时针旋转,得△AB'C',连接BB',若BB'∥AC,则∠BAC′的大小是( )
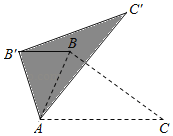
A.15°B.25°C.35°D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() ,点
,点![]() .
.
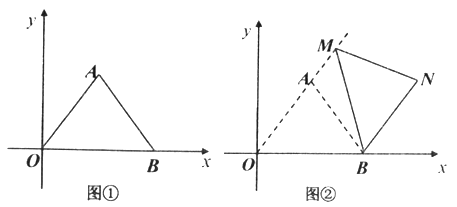
(Ⅰ)如图①,求AB的长;
(Ⅱ)如图②,把图①中的![]() 绕点B顺时针旋转,使点O的对应点AM恰好落在OA延长线上,N是点A旋转后的对应点.
绕点B顺时针旋转,使点O的对应点AM恰好落在OA延长线上,N是点A旋转后的对应点.
①求证:![]() ;②求点N的坐标;
;②求点N的坐标;
(Ⅲ)点C是OB的中点,点D为线段OA上的动点,在![]() 绕点B顺时针旋转过程中,点D的对应点是P,求线段CP长的取值范围(直接写出结果).
绕点B顺时针旋转过程中,点D的对应点是P,求线段CP长的取值范围(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
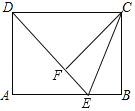
【题目】如图,矩形ABCD中,AB=4,AD=3,E是边AB上一点,将△CBE沿直线CE对折,得到△CFE,连接DF.
(1)当D、E、F三点共线时,证明:DE=CD;
(2)当BE=1时,求△CDF的面积;
(3)若射线DF交线段AB于点P,求BP的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了了解初中学校“高效课堂”的有效程度,并就初中生在课堂上是否具有“主动质疑”、“独立思考”、“专注听讲”、“讲解题目”等学习行为进行评价.为此,该市教研部门开展了一次抽样调查, 并将调查结果绘制成尚不完整的条形统计图和扇形统计图( 如图所示),请根据图中信息解答下列问题:
(1)这次抽样调查的样本容量为 .
(2)在扇形统计图中,“主动质疑”对应的圆心角为 度;
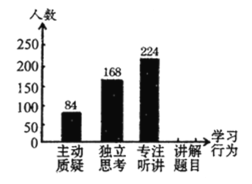
(3)请补充完整条形统计图;
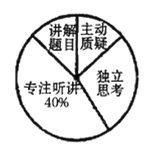
(4)若该市初中学生共有![]() 万人,在课堂上具有“独立思考”行为的学生约有多少人?
万人,在课堂上具有“独立思考”行为的学生约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com