
【题目】如图,平面直角坐标系中,一次函数y=x﹣1的图象与x轴,y轴分别交于点A,B,与反比例函数y=![]() 的图象交于点C,D,CE⊥x轴于点E,
的图象交于点C,D,CE⊥x轴于点E,![]() .
.
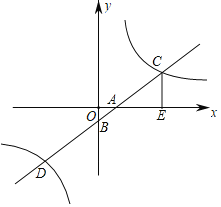
(1)求反比例函数的表达式与点D的坐标;
(2)以CE为边作ECMN,点M在一次函数y=x﹣1的图象上,设点M的横坐标为a,当边MN与反比例函数y=![]() 的图象有公共点时,求a的取值范围.
的图象有公共点时,求a的取值范围.
【答案】(1)D(﹣3,﹣4);(2)当边MN与反比例函数y=![]() 的图象有公共点时4<a≤6或﹣3<a≤﹣2.
的图象有公共点时4<a≤6或﹣3<a≤﹣2.
【解析】
(1)利用待定系数法以及等腰直角三角形的性质求出EC,OE即可解决问题.
(2)如图,设M(a,a﹣1),则N(a,![]() ),由EC=MN构建方程求出特殊点M的坐标即可判断.
),由EC=MN构建方程求出特殊点M的坐标即可判断.
解:(1)由题意A(1,0),B(0,﹣1),
∴OA=OB=1,
∴∠OAB=∠CAE=45°
∵AE=3OA,
∴AE=3,
∵EC⊥x轴,
∴∠AEC=90°,
∴∠EAC=∠ACE=45°,
∴EC=AE=3,
∴C(4,3),
∵反比例函数y=![]() 经过点C(4,3),
经过点C(4,3),
∴k=12,
由 ,解得
,解得![]() 或
或![]() ,
,
∴D(﹣3,﹣4).
(2)如图,设M(a,a﹣1),则N(a,![]() )
)

∵四边形ECMN是平行四边形,
∴MN=EC=3,
∴|a﹣1﹣![]() |=3,
|=3,
解得a=6或﹣2或﹣1±![]() (舍弃),
(舍弃),
∴M(6,5)或(﹣2,﹣3),
观察图象可知:当边MN与反比例函数y=![]() 的图象有公共点时4<a≤6或﹣3<a≤﹣2.
的图象有公共点时4<a≤6或﹣3<a≤﹣2.


科目:初中数学 来源: 题型:
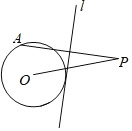
【题目】如图,⊙O的半径为4,点P是⊙O外的一点,PO=10,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丽江布农铃,是一种极富特色的、形状同马帮的马铃的挂件.这种马帮文化商品,是纯手工制作.精致小巧的青铜铃铛下系有一块圆形木块,手绘着各种各样的画.某商店需要购进甲、乙两种布农铃共300件,一件甲种布农铃进价为340元,售价为400元,一件乙种布农铃进价为380元,售价为460元.(注:利润=售价-进价)
(1)若商店计划销售完这批布农铃后能获利21600元,问甲、乙两种布农铃应分别购进多少件?
(2)若商店计划投入资金110000元,则能购进甲种布农铃多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任大叔决定在承包的荒山上种樱桃树,第一次用1000元购进了一批树苗,第二次又用1000元购进该种树苗,但这次每棵树苗的进价是第一次进价的2倍,购进数量比第次少了100棵;
(1)求第一次每棵树苗的进价是多少元?
(2)一年后,树苗的成活率为85%,每棵樱桃树平均产樱桃30斤,任大叔将两批樱桃树所产樱桃按同一价格全部销售完毕后,获利不低于89800元,求每斤樱桃的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
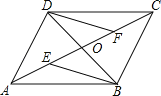
【题目】如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,AE=CF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)若OD=![]() AC,则四边形ABCD是什么特殊四边形?请证明你的结论.
AC,则四边形ABCD是什么特殊四边形?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
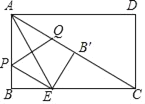
【题目】如图,矩形ABCD中,对角线AC=2![]() ,E为BC边上一点,BC=3BE,将矩形ABCD沿AE所在的直线折叠,点B恰好落在对角线AC上的点B′处,P,Q分别是AB,AC上的动点,则PE+PQ的最小值为( )
,E为BC边上一点,BC=3BE,将矩形ABCD沿AE所在的直线折叠,点B恰好落在对角线AC上的点B′处,P,Q分别是AB,AC上的动点,则PE+PQ的最小值为( )
A.![]() B.2C.1D.3
B.2C.1D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com