
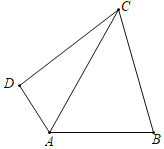
【题目】如图,在四边形ABCD中,∠DAB=120°,∠DCB=60°,CB=CD,AC=8,则四边形ABCD的面积为__.
【答案】16![]()
【解析】
延长AB至点E,使BE=DA,连接CE,作CF⊥AB于F,证明△CDA≌△CBE,根据全等三角形的性质得到CA=CE,∠BCE=∠DCA,得到△CAE为等边三角形,根据等边三角形的性质计算,得到答案.
延长AB至点E,使BE=DA,连接CE,作CF⊥AB于F,
∵∠DAB+∠DCB=120°+60°=180°,
∴∠CDA+∠CBA=180°,又∠CBE+∠CBA=180°,
∴∠CDA=∠CBE,
在△CDA和△CBE中,
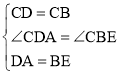 ,
,
∴△CDA≌△CBE(SAS)
∴CA=CE,∠BCE=∠DCA,
∵∠DCB=60°,
∴∠ACE=60°,
∴△CAE为等边三角形,
∴AE=AC=8,CF=![]() AC=4
AC=4![]() ,
,
则四边形ABCD的面积=△CAB的面积=![]() ×8×4
×8×4![]() =16
=16![]() ,
,
故答案为:16![]() .
.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
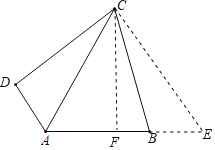
【题目】如图,在淮河的右岸边有一高楼,左岸边有一坡度![]() 的山坡
的山坡![]() ,点
,点![]() 与点
与点![]() 在同一水平面上,
在同一水平面上,![]() 与
与![]() 在同一平面内.某数学兴趣小组为了测量楼
在同一平面内.某数学兴趣小组为了测量楼![]() 的高度,在坡底
的高度,在坡底![]() 处测得楼顶
处测得楼顶![]() 的仰角为
的仰角为![]() ,然后沿坡面
,然后沿坡面![]() 上行了
上行了![]() 米到达点
米到达点![]() 处,此时在
处,此时在![]() 处测得楼顶
处测得楼顶![]() 的仰角为
的仰角为![]() ,求楼
,求楼![]() 的高度.(结果保留整数)(参考数
的高度.(结果保留整数)(参考数![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某童装店到厂家选购A、B两种服装.若购进A种服装12件、B种服装8件,需要资金1880元;若购进A种服装9件、B种服装10件,需要资金1810元.
(1)求A、B两种服装的进价分别为多少元?
(2)销售一件A服装可获利18元,销售一件B服装可获利30元.根据市场需求,服装店决定:购进A种服装的数量要比购进B种服装的数量的2倍还多4件,且A种服装购进数量不超过28件,并使这批服装全部销售完毕后的总获利不少于699元.设购进B种服装x件,那么:
①请写出A、B两种服装全部销售完毕后的总获利y元与x件之间的函数关系式;
②请问该服装店有几种满足条件的进货方案?哪种方案获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,
与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,![]() 且
且![]() .
.
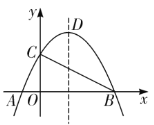
(1)求抛物线的解析式及点D的坐标;
(2)点P为y轴右侧抛物线上一点,是否存在点P使![]() ?若存在请求出点P坐标;若不存在请说明理由.
?若存在请求出点P坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,一次函数y=x﹣1的图象与x轴,y轴分别交于点A,B,与反比例函数y=![]() 的图象交于点C,D,CE⊥x轴于点E,
的图象交于点C,D,CE⊥x轴于点E,![]() .
.
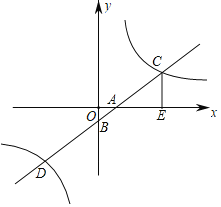
(1)求反比例函数的表达式与点D的坐标;
(2)以CE为边作ECMN,点M在一次函数y=x﹣1的图象上,设点M的横坐标为a,当边MN与反比例函数y=![]() 的图象有公共点时,求a的取值范围.
的图象有公共点时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+6与x轴、y轴交于A、B两点,点C在第四象限,BC⊥AB,且BC=AB;
x+6与x轴、y轴交于A、B两点,点C在第四象限,BC⊥AB,且BC=AB;
(1)如图1,求点C的坐标;
(2)如图2,D是BC的中点,过D作AC的垂线EF交AC于E,交直线AB于F,连接CF,点P为射线AD上一动点,求PF2﹣PC2的值;
(3)如图3,在(2)的条件下,在第二象限过点A作线段AM⊥AB于点A,在线段AB上取一点N,连接MN,使MN=BN,在第三象限取一点Q,使∠NMQ=90°,连接QC,若QC∥AB,且QC=6AM,设点P的横坐标为t,△PMQ的面积为s,求s与t的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M为线段AB的中点,AE与BD交于点C,![]() ,且DM交AC于F,ME交BC于点G.
,且DM交AC于F,ME交BC于点G.
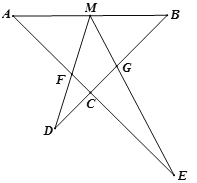
(1)写出图中相似三角形,并证明其中的一对;
(2)请连结FG,如果![]() ,
,![]() ,
,![]() ,求BG、FG的长.
,求BG、FG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com