练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，抛物线与x轴交于A、B两点，与y轴交于点C，其对称轴交抛物线于点D，且.

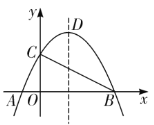
    （1）求抛物线的解析式及点D的坐标；

    （2）点P为y轴右侧抛物线上一点，是否存在点P使？若存在请求出点P坐标；若不存在请说明理由.

    【答案】（1），点D的坐标为；（2）点P的坐标为或或.

    【解析】

    （1）根据题意得出C、B两点坐标，然后代入原解析式建立方程组求解，之后进一步即可得出解析式，然后进一步配方即可得出点D坐标；

    （2）首先求出，然后设进一步根据题意建立方程求解即可.

    （1）由题意可得，，

    代入中，

    得解得

    ∴抛物线的解析式为.

    ∴

    ∴点D的坐标为；

    （2）存在点P使.

    ∵当时，或，

    ∴.

    ∴.

    设，

    ∵.

    ∴.

    ∴.

    ∴或.

    解得，，或（舍去），，

    ∴点P的坐标为或或.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，点A，C，D，B在以O点为圆心，OA长为半径的圆弧上， AC=CD=DB，AB交OC于点E．求证：AE=CD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，E、F、G、H分别是BD、BC、AC、AD的中点，且AB＝CD．下列结论：①EG⊥FH，②四边形EFGH是矩形，③HF平分∠EHG，④EG＝ (BC－AD)，⑤四边形EFGH是菱形．其中正确的个数是 ( )

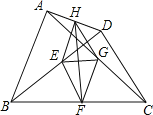
    A．1 B．2 C．3 D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法正确的是（ ）

    A．了解飞行员视力的达标率应使用抽样调查

    B．一组数据3，6，6，7，9的中位数是6

    C．从2000名学生中选200名学生进行抽样调查，样本容量为2000

    D．一组数据1，2，3，4，5的方差是10

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线L：y=﹣x2+bx+c经过点A（0，1），与它的对称轴直线x=1交于点B．

    （1）直接写出抛物线L的解析式；

    （2）如图1，过定点的直线y=kx﹣k+4（k＜0）与抛物线L交于点M、N．若△BMN的面积等于1，求k的值；

    （3）如图2，将抛物线L向上平移m（m＞0）个单位长度得到抛物线L1，抛物线L1与y轴交于点C，过点C作y轴的垂线交抛物线L1于另一点D．F为抛物线L1的对称轴与x轴的交点，P为线段OC上一点．若△PCD与△POF相似，并且符合条件的点P恰有2个，求m的值及相应点P的坐标．

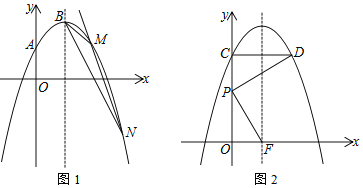
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，∠DAB＝120°，∠DCB＝60°，CB＝CD，AC＝8，则四边形ABCD的面积为__．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠ACB＝90°，∠B＝60°，AB＝4，D为AB中点，CE平分∠ACB，∠DEC＝30°，则CE＝_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

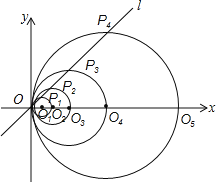
    【题目】如图，在平面直角坐标系中，直线l的函数表达式为y＝x，点O1的坐标为（1，0），以O1为圆心，O1O为半径画圆，交直线l于点P1，交x轴正半轴于点O2，以O2为圆心，O2O为半径画圆，交直线l于点P2，交x轴正半轴于点O3，以O3为圆心，O3O为半径画圆，交直线l于点P3，交x轴正半轴于点O4；…按此做法进行下去，其中的长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在同一平面直角坐标系中，函数y＝ax＋b与y＝ax2－bx的图象可能是（ ）

    A.B.C.D.

    查看答案和解析>>

    同步练习册答案