
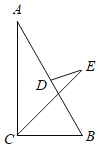
【题目】如图,△ABC中,∠ACB=90°,∠B=60°,AB=4,D为AB中点,CE平分∠ACB,∠DEC=30°,则CE=_____.
【答案】2![]()
【解析】
连接CD,作CH⊥DE于H,由直角三角形的性质可得CD=BD=AD=2,∠A=30°,可得HD=HC=![]() ,由直角三角形的性质可得CE=2HC=2
,由直角三角形的性质可得CE=2HC=2![]() .
.
解:连接CD,作CH⊥DE于H
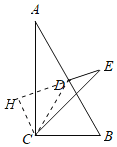
∵∠ACB=90°,∠B=60°,AB=4,D为AB中点,
∴CD=BD=AD=2,∠A=90°-60°=30°,
∴∠ACD=∠A=30°,
∵CE平分∠ACB,
∴∠ACE=45°,
∴∠DCE=15°,
∴∠HDC=∠DEC+∠DCE=45°,且CH⊥DE,
∴∠HCD=∠HDC=45°,且CD=2,
∴HD=HC=sin∠HDC·CH=![]() .
.
∵∠DEC=30°,CH⊥DE,
∴CE=2CH=2![]() .
.
故答案为:2![]() .
.


科目:初中数学 来源: 题型:
【题目】某景区为方便游客参观,在每个景点均设置两条通道,即楼梯和无障碍通道.如图,已知在某景点P处,供游客上下的楼梯倾斜角为30°(即∠PBA=30°),长度为4m(即PB=4m),无障碍通道PA的倾斜角为15°(即∠PAB=15°).求无障碍通道的长度.(结果精确到0.1m,参考数据:sin15°≈0.21,cos15°≈0.98)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组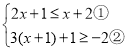 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得____________________;
(Ⅱ)解不等式②,得_______________________;
(III)把不等式①和②的解集在数轴上表示出来:

(IV)原不等式组的解集为________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,
与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,![]() 且
且![]() .
.
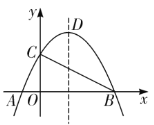
(1)求抛物线的解析式及点D的坐标;
(2)点P为y轴右侧抛物线上一点,是否存在点P使![]() ?若存在请求出点P坐标;若不存在请说明理由.
?若存在请求出点P坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=6,点M是BC的中点.
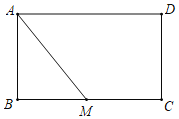
(1)在AM上求作一点E,使△ADE∽△MAB(尺规作图,不写作法);
(2)在(1)的条件下,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+6与x轴、y轴交于A、B两点,点C在第四象限,BC⊥AB,且BC=AB;
x+6与x轴、y轴交于A、B两点,点C在第四象限,BC⊥AB,且BC=AB;
(1)如图1,求点C的坐标;
(2)如图2,D是BC的中点,过D作AC的垂线EF交AC于E,交直线AB于F,连接CF,点P为射线AD上一动点,求PF2﹣PC2的值;
(3)如图3,在(2)的条件下,在第二象限过点A作线段AM⊥AB于点A,在线段AB上取一点N,连接MN,使MN=BN,在第三象限取一点Q,使∠NMQ=90°,连接QC,若QC∥AB,且QC=6AM,设点P的横坐标为t,△PMQ的面积为s,求s与t的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点F,C是⊙O上两点,且![]() ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
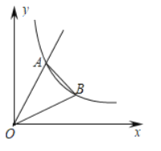
【题目】如图,正比例函数y1=k1x的图象与反比例函数y2=![]() (x>0)的图象相交于点A(
(x>0)的图象相交于点A(![]() ,2
,2![]() ),点B是反比例函数图象上一点,它的横坐标是3,连接OB,AB,则△AOB的面积是_____.
),点B是反比例函数图象上一点,它的横坐标是3,连接OB,AB,则△AOB的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市实验中学计划在暑假第二周的星期一至星期五开展暑假社会实践活动,要求每位学生选择两天参加活动.
(1)甲同学随机选择连续的两天,其中有一天是星期三的概率是 ;
(2)乙同学随机选择两天,其中有一天是星期三的概率是多少?(列表或画树形图或列举)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com