
����Ŀ����ͼ��ֱ��y��![]() x+6��x�ᡢy�ύ��A��B���㣬��C�ڵ������ޣ�BC��AB����BC��AB��
x+6��x�ᡢy�ύ��A��B���㣬��C�ڵ������ޣ�BC��AB����BC��AB��
��1����ͼ1�����C�����ꣻ
��2����ͼ2��D��BC���е㣬��D��AC�Ĵ���EF��AC��E����ֱ��AB��F������CF����PΪ����AD��һ���㣬��PF2��PC2��ֵ��
��3����ͼ3���ڣ�2���������£��ڵڶ�������A���߶�AM��AB�ڵ�A�����߶�AB��ȡһ��N������MN��ʹMN��BN���ڵ�������ȡһ��Q��ʹ��NMQ��90��������QC����QC��AB����QC��6AM�����P�ĺ�����Ϊt����PMQ�����Ϊs����s��t�ĺ�����ϵʽ��

���𰸡���1��C(6����2)����2��25����3��![]()
��������
��1����C��CH��y����H������BCH+��CBH��90����֤����BHC�ա�AOB��AAS�����ɽ�����⣻
��2����ͼ2�У�������AD��CF��G�����ݡ�SAS��֤����ABD�ա�CBF�����ù��ɶ���������⼴�ɣ�
��3����ͼ3�У�����BM��BQ����B��BK��QM�ӳ����ڵ�K���ӳ�MA��QC�ڵ�T���ɵ�������ABCT��֤����BKM�ա�BAM��ASA�����Ƴ�BA��BK��BC��MK��MA��֤��Rt��BKQ��Rt��BCQ��HL�����Ƴ�QK��QC����AM��a����QK��QC��6a����Rt��QMT�У�MQ��5a��MT��a+10��QT��6a��10�����ɶ����ɵ�a��![]() ����tan��MNA��tan��QMT��tan��BAO��
����tan��MNA��tan��QMT��tan��BAO��![]() ���Ƴ�QT��10��MQ��
���Ƴ�QT��10��MQ��![]() ��MT��
��MT��![]() ����PS��MQ�ڵ�S������
����PS��MQ�ڵ�S������![]() �����㼴�ɣ�
�����㼴�ɣ�
�⣺��1����ͼ1�У�
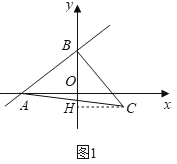
��y��![]() x+6����y��0����x����8����x��0����y��6
x+6����y��0����x����8����x��0����y��6
��A(��8��0)��B(0��6)��
��OA��8��OB��6��
��C��CH��y����H������BCH+��CBH��90����
��BC��AB��
���ABO+��CBH��90����
���BCH����ABO��
����BHC����AOB��90����BC��AB��
���BHC�ա�AOB��AAS����
��HC��OB��6��BH��OA��8��OH��8��6��2��
��C(6����2)��
��2����ͼ2�У�������AD��CF��G��
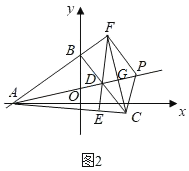
��BC��AB��BC��AB��
���BAC��45��
��EF��AC��
���AFE��45��
���BDF�ǵ���ֱ�������Σ�
��BD��BF��
����ABD����CBF��90����AB��CB
���ABD�ա�CBF��SAS����
���BAD����BCF��
�ߡ�BDA����CDG��
���CGD����ABD��90����
��AD��CF��
��OA��8��OB��6��
��AB��![]() ��10��
��10��
��BC��10��
��BF��BD��5��
��PF2��PC2��(PG2+FG2)��(PG2+CG2)
��FG2��CG2��(DF2��DG2)��(DC2��DG2)
��DF2��DC2��DF2��BD2��BF2��25
��3����ͼ3�У�����BM��BQ����B��BK��QM�ӳ����ڵ�K���ӳ�MA��QC�ڵ�T���ɵ�������ABCT��
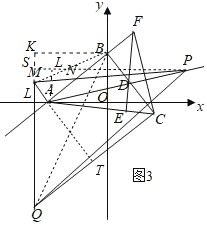
��MN��BN��
���NMB����NBM��
��BK��QK��NM��QK��
��BK��MN��
���KBM����BMN��
���KBM����MBA��
��MB��MB����K����BAM��90��
���BKM�ա�BAM��ASA����
��BA��BK��BC��MK��MA��
��Rt��BKQ��Rt��BCQ��HL����
��QK��QC��
��AM��a����QK��QC��6a��
��Rt��QMT�У�MQ��5a��MT��a+10��QT��6a��10�����ɶ����ɵ�a��![]() ��
��
��tan��MNA��tan��QMT��tan��BAO��![]() ��
��
��QT��10��MQ��![]() ��MT��
��MT��![]()
��MN��x�ᣬMQ��y�ᣬ��PS��MQ�ڵ�S��
��![]() ��
��
��MQ��x�ύ�ڵ�I��Rt��MAI�У�AI��2��
��AL��PS�ڵ�L���þ���ALSI��
��PS��PL+LS��t+10��
��![]() ��
��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
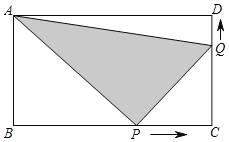
����Ŀ����ͼ���ھ���ABCD�У�AB=6cm��BC=12cm����P�ӵ�B�������߶�BC��CD��2cm/s���ٶ����յ�D�˶���ͬʱ����Q�ӵ�C�������߶�CD��DA��1cm/s���ٶ����յ�A�˶�(P��Q�����У�ֻҪ��һ�㵽���յ㣬����һ���˶�����ֹͣ)��
��1���˶�ֹͣ����һ���ȵ��յ㣿��һ�����յ㻹�ж�Զ��
��2�����˶������У���APQ������ܷ����22cm2�����ܣ����˶��ʱ�䣿�����ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A���˽����Ա�����Ĵ����Ӧʹ�ó�������
B��һ������3��6��6��7��9����λ����6
C����2000��ѧ����ѡ200��ѧ�����г������飬��������Ϊ2000
D��һ������1��2��3��4��5�ķ�����10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
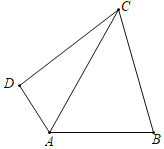
����Ŀ����ͼ�����ı���ABCD�У���DAB��120������DCB��60����CB��CD��AC��8�����ı���ABCD�����Ϊ__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
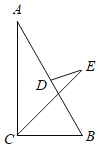
����Ŀ����ͼ����ABC�У���ACB��90������B��60����AB��4��DΪAB�е㣬CEƽ�֡�ACB����DEC��30������CE��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
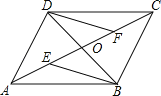
����Ŀ����ͼ���ı���ABCD�ĶԽ���AC��BD���ڵ�O����֪O��AC���е㣬AE=CF��DF��BE��
��1����֤����BOE�ա�DOF��
��2����OD=![]() AC�����ı���ABCD��ʲô�����ı��Σ���֤����Ľ��ۣ�
AC�����ı���ABCD��ʲô�����ı��Σ���֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
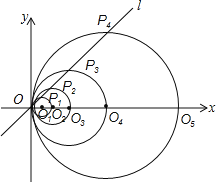
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l�ĺ�������ʽΪy��x����O1������Ϊ��1��0������O1ΪԲ�ģ�O1OΪ�뾶��Բ����ֱ��l�ڵ�P1����x���������ڵ�O2����O2ΪԲ�ģ�O2OΪ�뾶��Բ����ֱ��l�ڵ�P2����x���������ڵ�O3����O3ΪԲ�ģ�O3OΪ�뾶��Բ����ֱ��l�ڵ�P3����x���������ڵ�O4������������������ȥ������![]() �ij�Ϊ_____��
�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4����E��F�ֱ��ڱ�AB��AD�ϣ��ҡ�ECF��45�㣬CF���ӳ��߽�BA���ӳ����ڵ�G��CE���ӳ��߽�DA���ӳ����ڵ�H������AC��EF����GH��
��1����գ���AHC�� ����ACG�������������������
��2���߶�AC��AG��AHʲô��ϵ����˵�����ɣ�
��3����AE��m��
�١�AGH�����S�б仯������仯�������S��m�ĺ�����ϵʽ��������仯���������ֵ��
����ֱ��д��ʹ��CGH�ǵ��������ε�mֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
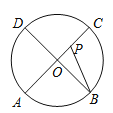
����Ŀ����ͼ����A��B��C��DΪ��O�ϵ��ĵȷֵ㣬����P��Բ��O��������O��C��D��O��·���������˶������˶���ʱ��Ϊt�룬��APB�Ķ���Ϊy��������ͼ���б�ʾy��t֮�亯����ϵ��ǡ�����ǣ�������
A. 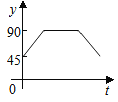 B.
B. 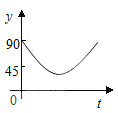 C.
C. 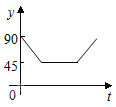 D.
D. 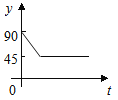
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com