

分析 (1)根据跳绳人数除以跳绳人数所占的百分比,可得抽测总人数,根据有理数的减法,可得参加篮球项目的人数,根据参加篮球项目的人数,可得答案;
(2)根据全校学生人数乘以参加篮球项目所占的百分比,可得答案.
解答 解:(1)20÷40%=50(人),
50-20-10-15=5(人),
∴小明所在的班级参加篮球项目的同学有5人,
正确补全图形
(2)800×$\frac{5}{50}$=80(人),
∴估计全校学生中有80人参加篮球项目.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:解答题
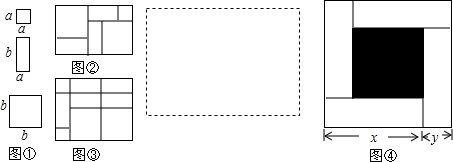
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
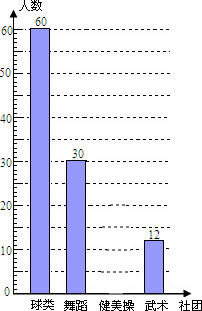 为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:| 社团类别 | 人数 | 占总人数比例 |
| 球类 | 60 | m |
| 舞蹈 | 30 | 0.25 |
| 健美操 | n | 0.15 |
| 武术 | 12 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
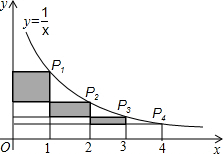 在反比例函数y=$\frac{1}{x}$(x>0)的图象上,有点P1,P2,…,P2011,…,它们的横坐标依次为1,2,…2011,…分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,…,S2010…,则S1+S2+…+S2010=$\frac{2010}{2011}$.
在反比例函数y=$\frac{1}{x}$(x>0)的图象上,有点P1,P2,…,P2011,…,它们的横坐标依次为1,2,…2011,…分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,…,S2010…,则S1+S2+…+S2010=$\frac{2010}{2011}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
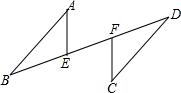 如图,AB∥CD,AB=CD,E,F是BD上的两点,要使△ABE≌△CDF(不再添加新的线段和字母),需添加的一个条件是BE=DF或∠A=∠C或∠AEB=∠CFD(只写一个条件即可).
如图,AB∥CD,AB=CD,E,F是BD上的两点,要使△ABE≌△CDF(不再添加新的线段和字母),需添加的一个条件是BE=DF或∠A=∠C或∠AEB=∠CFD(只写一个条件即可).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
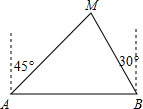 如图,A,B两个城市相距80km,现计划在这两座城市之间修建一条笔直的高速公路,经测量森林保护区中心M在城市A的北偏东45°和B城市的北偏西30°的方向上,已知森林保护区的范围在以M为圆心,以50km为半径的圆形区域内,请问计划修建的这条高速公路会不会穿过该森林保护区,为什么?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,A,B两个城市相距80km,现计划在这两座城市之间修建一条笔直的高速公路,经测量森林保护区中心M在城市A的北偏东45°和B城市的北偏西30°的方向上,已知森林保护区的范围在以M为圆心,以50km为半径的圆形区域内,请问计划修建的这条高速公路会不会穿过该森林保护区,为什么?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
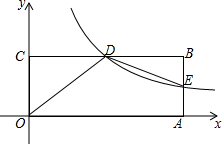 如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数图象交AB于E点,连接DE.若OD=5,tan∠COD=$\frac{4}{3}$.
如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数图象交AB于E点,连接DE.若OD=5,tan∠COD=$\frac{4}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com