
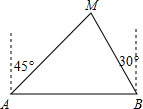
 ��ͼ��A��B�����������80km���ּƻ�������������֮����һ����ֱ�ĸ��ٹ�·��������ɭ�ֱ���������M�ڳ���A�ı�ƫ��45���B���еı�ƫ��30��ķ����ϣ���֪ɭ�ֱ������ķ�Χ����MΪԲ�ģ���50kmΪ�뾶��Բ�������ڣ����ʼƻ������������ٹ�·��ᴩ����ɭ�ֱ�������Ϊʲô�����ο����ݣ�$\sqrt{2}$��1.414��$\sqrt{3}$��1.732��
��ͼ��A��B�����������80km���ּƻ�������������֮����һ����ֱ�ĸ��ٹ�·��������ɭ�ֱ���������M�ڳ���A�ı�ƫ��45���B���еı�ƫ��30��ķ����ϣ���֪ɭ�ֱ������ķ�Χ����MΪԲ�ģ���50kmΪ�뾶��Բ�������ڣ����ʼƻ������������ٹ�·��ᴩ����ɭ�ֱ�������Ϊʲô�����ο����ݣ�$\sqrt{2}$��1.414��$\sqrt{3}$��1.732�� ���� ����M��MH��ֱ��AB������ΪH����MH=x��AH��BH�����Ը������Ǻ�����MH��ʾ����������AB�ij����õ�һ������x�ķ��̣����c�ij����Ӷ��жϳ��������ٹ�·��ᴩԽ�˷�������
��� 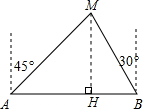 �⣺����M��MH��ֱ��AB������ΪH��
�⣺����M��MH��ֱ��AB������ΪH��
��MH=x��
��Rt��AMH��AH=MH=x��
��Rt��BHM��tan30��=$\frac{BH}{MH}$=$\frac{\sqrt{3}}{3}$����BH=$\frac{\sqrt{3}}{3}$x��
��AH+BH=80��
��x+$\frac{\sqrt{3}}{3}$x=80��
��� x=120-40$\sqrt{3}$��50.72��50��
�����������ٹ�·���ᴩ����ɭ�ֱ�������
���� ������Ҫ�����ֱ�������ε�Ӧ�ã���һ�������ε�����һ�����ת��Ϊ��ֱ�������ε����⣬����ķ������������ߣ�


 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
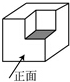 ��ͼ�ļ���������һ����������ȥһ��С�������γɵģ���������ͼ�ǣ�������
��ͼ�ļ���������һ����������ȥһ��С�������γɵģ���������ͼ�ǣ�������| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �٢ڢ� | C�� | �ۢ� | D�� | �٢ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -5 | B�� | 5 | C�� | -7 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{9}$=��3 | B�� | a8��a4=a2 | C�� | 3$\sqrt{2}-\sqrt{2}$=3 | D�� | a2•a3=a5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com