
| A. | ①② | B. | ①②③ | C. | ③④ | D. | ①②④ |
分析 根据方程解的定义对①进行判断;先得到当m=0时,函数解析式为y=-x+1,则可计算出(x1-x2)(y1-y2)=-(x1-x2)2,于是可根据非负数的性质对②进行判断;当m=-1时,解析式为y=-x2+x,可计算出y1+y2=2x1x2≠0,于是可对③进行判断;先计算出顶点坐标,然后根据一次函数图象上点的坐标特征对④进行判断.
解答 解:当x=1时,y=mx2-(2m+1)x+m+1=m-2m-1+m+1=0,则方程mx2-(2m+1)x+m+1=0必有一个根为x=1,所以①正确;
当m=0时,y=-x+1,则y1=-x1+1,y2=-x2+1,所以(x1-x2)(y1-y2)=(x1-x2)(-x1+x2)=-(x1-x2)2,而点P(x1,y1)和点Q(x2,y2)是两个不同的点,则(x1-x2)(y1-y2)=-(x1-x2)2<0,所以②正确;
当m=-1时,y=-x2+x,则y1=-x12+x1,y2=-x22+x2,所以y1+y2=-x12+x1-x22+x2=-(x1+x2)2+2x1x2+(x1+x2)=2x1x2≠0,所以③错误;
当m≠0时,顶点的横坐标为$\frac{2m+1}{2m}$,纵坐标为$\frac{4m(m+1{)-(2m+1)}^{2}}{4m}$=$\frac{-1}{4m}$,当x=$\frac{2m+1}{2m}$时,y=-$\frac{1}{2}$x+1=-$\frac{1}{2}$•$\frac{2m+1}{2m}$+1=$\frac{2m-1}{4m}$,所以抛物线的顶点不在直线y=-$\frac{1}{2}$x+1上,所以④错误.
故选A.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了二次函数的性质、方程解的定义和一次函数图象上点的坐标特征.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:解答题
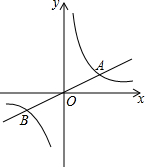 如图,已知直线y1=$\frac{1}{2}$x与双曲线y2=$\frac{k}{x}$(k>0)交于A、B两点,且点A的横坐标为4.
如图,已知直线y1=$\frac{1}{2}$x与双曲线y2=$\frac{k}{x}$(k>0)交于A、B两点,且点A的横坐标为4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
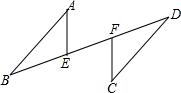 如图,AB∥CD,AB=CD,E,F是BD上的两点,要使△ABE≌△CDF(不再添加新的线段和字母),需添加的一个条件是BE=DF或∠A=∠C或∠AEB=∠CFD(只写一个条件即可).
如图,AB∥CD,AB=CD,E,F是BD上的两点,要使△ABE≌△CDF(不再添加新的线段和字母),需添加的一个条件是BE=DF或∠A=∠C或∠AEB=∠CFD(只写一个条件即可).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
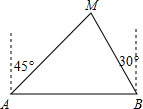 如图,A,B两个城市相距80km,现计划在这两座城市之间修建一条笔直的高速公路,经测量森林保护区中心M在城市A的北偏东45°和B城市的北偏西30°的方向上,已知森林保护区的范围在以M为圆心,以50km为半径的圆形区域内,请问计划修建的这条高速公路会不会穿过该森林保护区,为什么?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,A,B两个城市相距80km,现计划在这两座城市之间修建一条笔直的高速公路,经测量森林保护区中心M在城市A的北偏东45°和B城市的北偏西30°的方向上,已知森林保护区的范围在以M为圆心,以50km为半径的圆形区域内,请问计划修建的这条高速公路会不会穿过该森林保护区,为什么?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | {1,2} | B. | {1,4,7} | C. | {1,7,8} | D. | {-2,6} |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
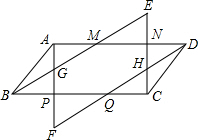 如图,四边形ABCD是平行四边形,AF∥CE,BE∥DF,AF交BE于G点,交DF于F点,CE交DF于H点、交BE于E点.
如图,四边形ABCD是平行四边形,AF∥CE,BE∥DF,AF交BE于G点,交DF于F点,CE交DF于H点、交BE于E点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com