
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:解答题
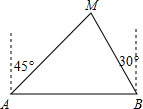 如图,A,B两个城市相距80km,现计划在这两座城市之间修建一条笔直的高速公路,经测量森林保护区中心M在城市A的北偏东45°和B城市的北偏西30°的方向上,已知森林保护区的范围在以M为圆心,以50km为半径的圆形区域内,请问计划修建的这条高速公路会不会穿过该森林保护区,为什么?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,A,B两个城市相距80km,现计划在这两座城市之间修建一条笔直的高速公路,经测量森林保护区中心M在城市A的北偏东45°和B城市的北偏西30°的方向上,已知森林保护区的范围在以M为圆心,以50km为半径的圆形区域内,请问计划修建的这条高速公路会不会穿过该森林保护区,为什么?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
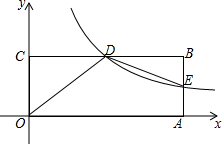 如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数图象交AB于E点,连接DE.若OD=5,tan∠COD=$\frac{4}{3}$.
如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数图象交AB于E点,连接DE.若OD=5,tan∠COD=$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
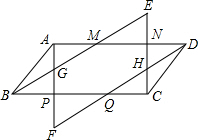 如图,四边形ABCD是平行四边形,AF∥CE,BE∥DF,AF交BE于G点,交DF于F点,CE交DF于H点、交BE于E点.
如图,四边形ABCD是平行四边形,AF∥CE,BE∥DF,AF交BE于G点,交DF于F点,CE交DF于H点、交BE于E点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
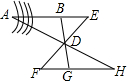 如图所示,要测量AB的长,因为无法过河接近点A,可以作AB外任取一点D,在AB的延长线上任取一点E,连接ED和BD,并且延长BD到G,使DG=BD,延长ED到F,使DF=ED,连接FG,并延长FG到H,使H、D、A在一直线上,则HG=AB,试说明这种测量方法的原理.
如图所示,要测量AB的长,因为无法过河接近点A,可以作AB外任取一点D,在AB的延长线上任取一点E,连接ED和BD,并且延长BD到G,使DG=BD,延长ED到F,使DF=ED,连接FG,并延长FG到H,使H、D、A在一直线上,则HG=AB,试说明这种测量方法的原理.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
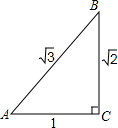 如图,已知Rt△ABC边长分别为1,$\sqrt{2}$,$\sqrt{3}$,则下列三角函数表示正确的是( )
如图,已知Rt△ABC边长分别为1,$\sqrt{2}$,$\sqrt{3}$,则下列三角函数表示正确的是( )| A. | sinA=$\frac{{\sqrt{3}}}{2}$ | B. | cosA=$\frac{{\sqrt{6}}}{3}$ | C. | tanA=$\sqrt{2}$ | D. | tanA=$\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com