
����Ŀ����֪����������A��B���㣬��A��ʾ����Ϊ4����B��A�����ߣ���AB=12������һ����P�������ϵ�A��������ÿ��1����λ���ȵ��ٶ����������������˶�������Q�ӵ�B��������ÿ��2����λ���ȵ��ٶ������������������˶������˶�ʱ��Ϊt�룮
![]()
(1)д�������ϵ�B��ʾ����Ϊ________��P����ʾ����Ϊ________(�ú�t�Ĵ���ʽ��ʾ)��
(2)����P��Q�ֱ��A��B����ͬʱ�������ʵ�P�˶���������Q���3����λ����?
(3)����P��Q�ֱ��A��B����ͬʱ�������ֱ���BQ��APΪ�ߣ��������Ϸ���������BQCD��������APEF��ͼ��ʾ.��tΪ��ֵʱ�����������ε��ص����������������APEF�����һ�룿��ֱ��д�����ۣ�t=__________��.

���𰸡�(1)-8��4-t��(2)3��5��(3)4.8��24.
��������
��1��������֪�ɵ�B���ʾ����Ϊ4-12����P��ʾ����Ϊ4-t��
��2�� ���P�˶�x��ʱ����Q���3����λ���ȣ������������P����Q���Ҳ࣬P����Q����࣬�ֱ��г����̼�����⣻
��3���ɷ������������ͼһ��P��Q���߶�AB�ϣ���ͼ����P��Q���߶�AB�⣬���������г�����t�ķ��̼������.
(1)�ߵ�A��ʾ����Ϊ4��B��A����ߣ�AB=12��
���B��ʾ������412=8��
�߶���P�ӵ�A��������ÿ��1����λ���ȵ��ٶ����������������˶���
���P��ʾ������4t.
(2)���P�˶�x��ʱ����Q���3����λ���ȣ������������
![]()
P����Q���Ҳ�ʱ��
��AP=x��BQ=2x��
��AP+BQ=AB3��
��x+2x=9��
��ã�x=3��
![]()
P����Q�����ʱ��
��AP+BQ=AB+3��
��x+2x=15
��ã�x=5.
���P�˶�3���5��ʱ���Q���3����λ���ȡ�
(3) �����������
��ͼһ�� 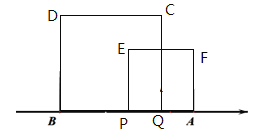
ͼһ
�����������ε��ص����������������APEF�����һ��,AP=t,BQ=2t,
��AQ=PQ=![]() ,
,
��2t+![]() =12 ���t=4.8
=12 ���t=4.8
��ͼ����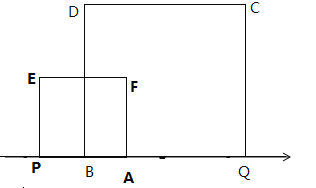
ͼ��
�����������ε��ص����������������APEF�����һ��,AP=t,BQ=2t,
��AB=PB=![]() ,
,
��![]() =12 ���t=24.
=12 ���t=24.
�ʴ�Ϊ��(1)-8��4-t��(2)3��5��(3)4.8��24.


 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Сѧȫ�濪չ���������������ijУ�ڴ�μ��п�����A����٣�B���ܲ٣�C���赸��D��������������Ϊ�˽�ѧ����ϲ����һ���������ȡ�˲���ѧ�����е��飬�������������Ƴ�������������������ͳ��ͼ�������ͳ��ͼ�ش��������⣺ 
��1����α������ѧ�������ˣ�
��2���뽫ͳ��ͼ2����������
��3��ͳ��ͼ1��B��Ŀ��Ӧ�����ε�Բ�Ľ����ȣ�
��4����֪��У����ѧ��3600�ˣ�����ݵ��������Ƹ�Уϲ�������ٵ�ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������й���ͳ��ѧ����Ҫ���������춨���й���ͳ��ѧ�Ļ�����ܣ����Ĵ����ɾ���Ҫ�������������������ͷ����������У��������ǡ�������������ߵ���ѧ�ɾͣ��������������м��أ��������˹����˳��ţ�ӯʮһ���˳���������ʮ�������������Σ���
���ģ����м����˹�ͬ��Ǯ�����ÿ�˳���Ǯ����ô����ʮһǮ�����ÿ�˳���Ǯ����ô����ʮ��Ǯ���ʣ��м����˹�ͬ��Ǯ������x���˹�ͬ������������һԪһ�η��̣�_____

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ,
,![]() ,����
,����![]() ������Ϊ
������Ϊ![]() �����ӳ�
�����ӳ�![]() ��ʹ
��ʹ![]() ������
������![]() .
.
��1����֤���ı���![]() ��ƽ���ı��Ρ�
��ƽ���ı��Ρ�
��2������![]() �����
�����![]()

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
��������2�멁1���Ե�����֮��ľ��룺|2��(��1)|=3��
�������ϩ�2��3���Ե�����֮��ľ��룺|��2��3|=5��
�������ϩ�3�멁1���Ե�����֮��ľ��룺|(��1)��(��3)|=2
���ɣ��������ϵ�A��B�ֱ��ʾ��a��b����A��B����֮��ľ���AB=|a��b|��|b��a|

�ش��������⣺
(1) �����ϱ�ʾ��x��1������֮��ľ����ʾΪ�� ���������ϱ�ʾ��x���� ��������֮��ľ����ʾΪ|x+2|��
(2)�����ڲݸ�ֽ�ϻ������ᣬ����ʾ��x�ĵ��ک�2��3֮���ƶ�ʱ��|x��3|+|x+2|��ֵ����һ���̶���ֵΪ���� ����
(3)���������ڲݸ�ֽ�ϻ������ᣬ̽����x=_______ʱ��|x-3|+|x+2|=7.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ƹ�������������μ䡱�������ij��ѧ������ѧ���п���A��ʵ����B��������Զ��C��������D���ܲ����ֻ��Ŀ��Ϊ���˽�ѧ����������Ŀ��ϲ������������ȡ�˲���ѧ�����е��飬�������������Ƴ���ͼ�٢ڵ�ͳ��ͼ������ͼ�е���Ϣ����������⣺ 
��1������������У��������˶�����ѧ����
��2������㱾�������ϲ����������Զ����ѧ����������ռ�ٷֱȣ���������ͳ��ͼ����������
��3�������鵽ϲ������������5��ѧ������3��������2��Ů�����ִ���5��ѧ���������ȡ2��ѧ�������û���״ͼ���б��ķ���������պó鵽ͬ�Ա�ѧ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺�������һԪһ�η��̵Ľ⻥Ϊ�෴�������Ǿͳ�����������Ϊ���ֵܷ��̡���
�緽��2x��4��3x+6��0Ϊ���ֵܷ��̡���
��1��������x�ķ���5x+m��0�뷽��2x��4��x+1�ǡ��ֵܷ��̡�����m��ֵ��
��2�����������ֵܷ��̡���������IJ�Ϊ8������һ����Ϊn����n��ֵ��
��3��������x�ķ���2x+3m��2��0��3x��5m+4��0�ǡ��ֵܷ��̡��������������̵Ľ⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90����AC=BC������C����ABC����ֱ��MN��AM��MN��M��BN��MN��N��
��1����֤��MN=AM+BN��

��2��������C����ABC����ֱ��MN��AM��MN��M��BN��MN��N����AM��BN��MN֮����ʲô��ϵ����˵�����ɡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ʾ����֪MN��PQ����B��MN�ϣ���C��PQ�ϣ���A�ڵ�B����࣬��D�ڵ�C���Ҳ࣬��ADC����ABC��ƽ�����ཻ�ڵ�E(����B��D���غ�)����CBN��110��.
(1)����ADQ��140�㣬д����BED�Ķ��� (ֱ��д���������)��
(2)����ADQ��m�㣬���߶�AD��DC����ƽ�ƣ�ʹ��D�ƶ�����C����࣬�����������䣬��ͼ����ʾ�����BED�Ķ���(�ú�m��ʽ�ӱ�ʾ)��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com