
【题目】在国家的宏观调控下,某市的商品房成交价由去年![]() 月份的
月份的![]() 元
元![]() 下降到
下降到![]() 月份的
月份的![]() 元
元![]() .
.
![]() 求
求![]() 、
、![]() 两月平均每月降价的百分率是多少?
两月平均每月降价的百分率是多少?
![]() 如果房价继续回落,按此降价的百分率,你预测到今年
如果房价继续回落,按此降价的百分率,你预测到今年![]() 月份该市的商品房成交均价是否会跌破
月份该市的商品房成交均价是否会跌破![]() 元
元![]() ?请说明理由.
?请说明理由.
【答案】(1)![]() 、
、![]() 两月平均每月降价的百分率是
两月平均每月降价的百分率是![]() ;
;![]() 不会跌破
不会跌破![]() 元
元![]() .
.
【解析】
(1)设11、12两月平均每月降价的百分率是x,那么4月份的房价为14000(1-x),12月份的房价为14000(1-x)2,然后根据12月份的11340元/m2即可列出方程解决问题;
(2)根据(1)的结果可以计算出今年2月份商品房成交均价,然后和10000元/m2进行比较即可作出判断.
(1)设11、12两月平均每月降价的百分率是x,
则11月份的成交价是:14000(1-x),
12月份的成交价是:14000(1-x)2,
∴14000(1-x)2=11340,
∴(1-x)2=0.81,
∴x1=0.1=10%,x2=1.9(不合题意,舍去)
答:11、12两月平均每月降价的百分率是10%;
(2)会跌破10000元/m2.
如果按此降价的百分率继续回落,估计今年2月份该市的商品房成交均价为:
11340(1-x)2=11340×0.81=9184.5<10000,
由此可知今年2月份该市的商品房成交均价会跌破10000元/m2.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
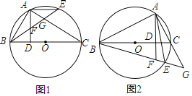
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,
上,![]() ,垂足为
,垂足为![]() ,弧
,弧![]() 等于弧
等于弧![]() ,
,![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
![]() 判断
判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 若点
若点![]() 和点
和点![]() 在
在![]() 的两侧,
的两侧,![]() 、
、![]() 的延长线交于点
的延长线交于点![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,其余条件不变,
,其余条件不变,![]() 中的结论还成立吗?请说明理由.
中的结论还成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
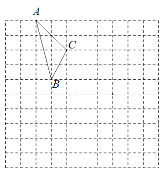
【题目】如图,在平面直角坐标系中,已知△ ABC 的三个顶点的坐标分别为 A(-3,5),B(-2,1).
(1)请在如图所示的网格内画出平面直角坐标系,并写出 C 点坐标;
(2)先将△ABC 沿 x 轴翻折,再沿 x 轴向右平移 4 个单位长度后得到△A1B1C1,请 在网格内画出△A1B1C1;
(3)在(2)的条件下,△ABC 的边 AC 上一点 M(a,b)的对应点 M1 的坐标是 .(友情提醒:画图结果确定后请用黑色签字笔加黑)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=90°.
(1)尺规作图:按下列要求完成作图(保留作图痕迹,请标明字母)
①作线段AC的垂直平分线l,交AC于点O;
②连接BO并延长,在BO的延长线上截取OD,使得OD=OB;
③连接DA、DC.
(2)判断四边形ABCD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个长方形的面积为6,它的一边为x,它的另一边长为y,周长为p.
(1)填空:(用含x的代数式表示)
① y=__________;② p=__________;
(2)当x值从2增大到a+2时,y的值减少了2,求增量a的值;
(3)当x=m时,p的值为![]() ;当
;当![]() 时,p的值为
时,p的值为![]() ,求
,求![]() 的值,并化成最简分式.
的值,并化成最简分式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,E为CD上一点,F为BC延长线上一点,且CE=CF.
(1)求证:△BCE≌△DCF;
(2)若∠FDC=30°,求∠BEF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
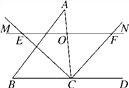
【题目】如图,在△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)探究线段OE与OF的数量关系并加以证明;
(2)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?并说明理由;
(3)当点O在边AC上运动时,四边形BCFE可能是菱形吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
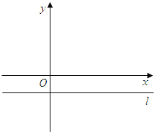
【题目】已知二次函数图象的顶点在原点![]() ,对称轴为
,对称轴为![]() 轴.一次函数
轴.一次函数![]() 的图象与二次函数的图象交于
的图象与二次函数的图象交于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 的左侧),且
的左侧),且![]() 点坐标为
点坐标为![]() .平行于
.平行于![]() 轴的直线
轴的直线![]() 过
过![]() 点.
点.
![]() 求一次函数与二次函数的解析式;
求一次函数与二次函数的解析式;
![]() 判断以线段
判断以线段![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系,并给出证明;
的位置关系,并给出证明;
![]() 把二次函数的图象向右平移
把二次函数的图象向右平移![]() 个单位,再向下平移
个单位,再向下平移![]() 个单位
个单位![]() ,二次函数的图象与
,二次函数的图象与![]() 轴交于
轴交于![]() ,
,![]() 两点,一次函数图象交
两点,一次函数图象交![]() 轴于
轴于![]() 点.当
点.当![]() 为何值时,过
为何值时,过![]() ,
,![]() ,
,![]() 三点的圆的面积最小?最小面积是多少?
三点的圆的面积最小?最小面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(材料阅读)我们曾解决过课本中的这样一道题目:
如图,四边形![]() 是正方形,
是正方形,![]() 为
为![]() 边上一点,延长
边上一点,延长![]() 至
至![]() ,使
,使![]() ,连接
,连接![]() .……
.……
提炼1:![]() 绕点
绕点![]() 顺时针旋转90°得到
顺时针旋转90°得到![]() ;
;
提炼2:![]() ;
;
提炼3:旋转、平移、轴对称是图形全等变换的三种方式.
![]()
(问题解决)(1)如图,四边形![]() 是正方形,
是正方形,![]() 为
为![]() 边上一点,连接
边上一点,连接![]() ,将
,将![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在
落在![]() 处,
处,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .可得:
.可得:![]() °;
°;![]() 三者间的数量关系是
三者间的数量关系是

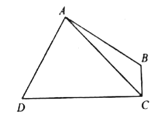
(2)如图,四边形![]() 的面积为8,
的面积为8,![]() ,
,![]() ,连接
,连接![]() .求
.求![]() 的长度.
的长度.
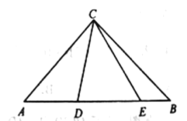
(3)如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() .写出
.写出![]() 间的数量关系,并证明.
间的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com