
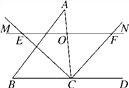
【题目】如图,在△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)探究线段OE与OF的数量关系并加以证明;
(2)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?并说明理由;
(3)当点O在边AC上运动时,四边形BCFE可能是菱形吗?说明理由.
【答案】(1)OE=OF.证明见解析;(2)四边形AECF是正方形;理由见解析;(3)四边形BCFE不可能为菱形.理由见解析.
【解析】
试题(1)由直线MN∥BC,MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,易证得△OEC与△OFC是等腰三角形,则可证得OE=OF=OC;
(2)正方形的判定问题,AECF若是正方形,则必有对角线OA=OC,所以O为AC的中点,同样在△ABC中,当∠ACB=90°时,可满足其为正方形;
(3)菱形的判定问题,若使菱形,则必有四条边相等,对角线互相垂直.
试题解析:(1)OE=OF.理由如下:
∵CE是∠ACB的角平分线,
∴∠ACE=∠BCE,
又∵MN∥BC,
∴∠NEC=∠ECB,
∴∠NEC=∠ACE,
∴OE=OC,
∵OF是∠BCA的外角平分线,
∴∠OCF=∠FCD,
又∵MN∥BC,
∴∠OFC=∠ECD,
∴∠OFC=∠COF,
∴OF=OC,
∴OE=OF;
(2)当点O运动到AC的中点,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.理由如下:
∵当点O运动到AC的中点时,AO=CO,
又∵EO=FO,
∴四边形AECF是平行四边形,
∵FO=CO,
∴AO=CO=EO=FO,
∴AO+CO=EO+FO,即AC=EF,
∴四边形AECF是矩形.
已知MN∥BC,当∠ACB=90°,则
∠AOF=∠COE=∠COF=∠AOE=90°,
∴AC⊥EF,
∴四边形AECF是正方形;
(3)不可能.理由如下:如图,
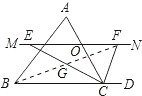
∵CE平分∠ACB,CF平分∠ACD,
∴∠ECF=![]() ∠ACB+
∠ACB+![]() ∠ACD=
∠ACD=![]() (∠ACB+∠ACD)=90°,
(∠ACB+∠ACD)=90°,
若四边形BCFE是菱形,则BF⊥EC,
但在△GFC中,不可能存在两个角为90°,所以不存在其为菱形.
故答案为不可能.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点C在AB上,![]() 、
、![]() 均是等边三角形,
均是等边三角形,![]() 、
、![]() 分别与
分别与![]() 交于点
交于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() 为等边三角形;④
为等边三角形;④![]() ∥
∥![]() ;⑤DC=DN正确的有( )个
;⑤DC=DN正确的有( )个
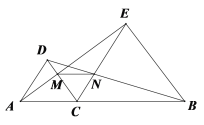
A.2个B.3个C.4个D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家的宏观调控下,某市的商品房成交价由去年![]() 月份的
月份的![]() 元
元![]() 下降到
下降到![]() 月份的
月份的![]() 元
元![]() .
.
![]() 求
求![]() 、
、![]() 两月平均每月降价的百分率是多少?
两月平均每月降价的百分率是多少?
![]() 如果房价继续回落,按此降价的百分率,你预测到今年
如果房价继续回落,按此降价的百分率,你预测到今年![]() 月份该市的商品房成交均价是否会跌破
月份该市的商品房成交均价是否会跌破![]() 元
元![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
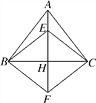
【题目】如图,在等腰三角形ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.
(1)求证:四边形EBFC是菱形;
(2)如果∠BAC=∠ECF,求证:AC⊥CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y1=kx+m和二次函数y2=ax2+bx+c的图象如图所示,它们的两个交点的横坐标是1和4,那么能够使得y1<y2的自变量x的取值范围是 .
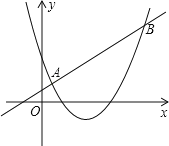
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() ,直线
,直线![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() 分别与
分别与![]() 轴相交于点
轴相交于点![]() .
.
(1)求点P的坐标.
(2)若![]() ,求x的取值范围.
,求x的取值范围.
(3)点![]() 为x轴上的一个动点,过
为x轴上的一个动点,过![]() 作x轴的垂线分别交
作x轴的垂线分别交![]() 和
和![]() 于点
于点![]() ,当EF=3时,求m的值.
,当EF=3时,求m的值.
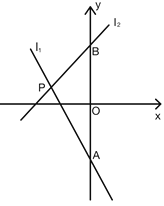
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(l)观察猜想:如图①,点![]() 、
、![]() 、
、![]() 在同一条直线上,
在同一条直线上,![]() ,
,![]() 且
且![]() ,
,![]() ,则
,则![]() 和
和![]() 是否全等?__________(填是或否),线段
是否全等?__________(填是或否),线段![]() 之间的数量关系为__________
之间的数量关系为__________
(2)问题解决:如图②,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 为直角边向外作等腰
为直角边向外作等腰![]() ,连接
,连接![]() ,求
,求![]() 的长。
的长。
(3)拓展延伸:如图③,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 于点
于点![]() .求
.求![]() 的长.
的长.
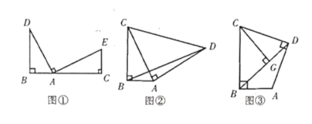
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com