
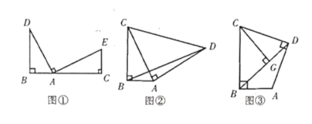
【题目】(l)观察猜想:如图①,点![]() 、
、![]() 、
、![]() 在同一条直线上,
在同一条直线上,![]() ,
,![]() 且
且![]() ,
,![]() ,则
,则![]() 和
和![]() 是否全等?__________(填是或否),线段
是否全等?__________(填是或否),线段![]() 之间的数量关系为__________
之间的数量关系为__________
(2)问题解决:如图②,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 为直角边向外作等腰
为直角边向外作等腰![]() ,连接
,连接![]() ,求
,求![]() 的长。
的长。
(3)拓展延伸:如图③,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 于点
于点![]() .求
.求![]() 的长.
的长.
【答案】(1)是,![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据垂直的定义,直角三角形的性质证得∠D=∠CAE,即可利用AAS证明△BAD≌△CEA,即可得到答案;
(2)过![]() 作
作![]() ,交
,交![]() 的延长线于
的延长线于![]() ,利用勾股定理求出BC,根据(1)得到
,利用勾股定理求出BC,根据(1)得到![]() ,再利用勾股定理求出BD;
,再利用勾股定理求出BD;
(3)过![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]() ,连接
,连接![]() ,利用勾股定理求出BC,证明
,利用勾股定理求出BC,证明![]() 得到四边形BEFD是正方形,即可求出CG.
得到四边形BEFD是正方形,即可求出CG.
(1)∵![]() ,
,![]() ,
,
∴∠B=∠C=![]() ,
,
∴∠BAD+∠D=∠BAD+∠CAE=90![]() ,
,
∴∠D=∠CAE,
∵![]() ,
,
∴△BAD≌△CEA,
∴AB=CE,BD=AC,
故答案为:是,![]() ;
;
(2)问题解决
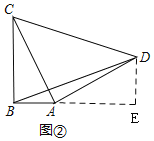
如图②,过![]() 作
作![]() ,交
,交![]() 的延长线于
的延长线于![]() ,
,
由(1)得:![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:![]()
![]() ,
,
![]() 中,
中,![]() ,
,
由勾股定理得: ![]()
(3)拓展延伸
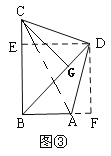
如图③,过![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]() ,连接
,连接![]()
∵![]() ,
,![]() ,
,![]() ,
,
∴AC=13,
∵![]() ,
,
∴BC=12,
∵![]() ,
,![]() ,
,
∴∠DEB=∠DFB=90![]() ,
,
∴四边形BEFD是矩形,
∴∠EDF=90![]() ,
,
∴∠EDC=∠ADF,
∴![]() ,
,
∴ED=DF,
∴四边形BEFD是正方形,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
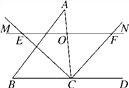
【题目】如图,在△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)探究线段OE与OF的数量关系并加以证明;
(2)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?并说明理由;
(3)当点O在边AC上运动时,四边形BCFE可能是菱形吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
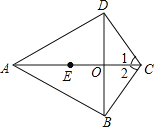
【题目】如图,在四边形ABCD中,AB=AD,BC=DC,AC、BD相交于点O,点E在AO上,且OE=OC.
(1)求证:∠1=∠2;
(2)连结BE、DE,判断四边形BCDE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(材料阅读)我们曾解决过课本中的这样一道题目:
如图,四边形![]() 是正方形,
是正方形,![]() 为
为![]() 边上一点,延长
边上一点,延长![]() 至
至![]() ,使
,使![]() ,连接
,连接![]() .……
.……
提炼1:![]() 绕点
绕点![]() 顺时针旋转90°得到
顺时针旋转90°得到![]() ;
;
提炼2:![]() ;
;
提炼3:旋转、平移、轴对称是图形全等变换的三种方式.
![]()
(问题解决)(1)如图,四边形![]() 是正方形,
是正方形,![]() 为
为![]() 边上一点,连接
边上一点,连接![]() ,将
,将![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在
落在![]() 处,
处,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .可得:
.可得:![]() °;
°;![]() 三者间的数量关系是
三者间的数量关系是

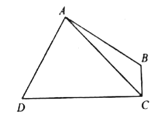
(2)如图,四边形![]() 的面积为8,
的面积为8,![]() ,
,![]() ,连接
,连接![]() .求
.求![]() 的长度.
的长度.
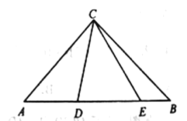
(3)如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() .写出
.写出![]() 间的数量关系,并证明.
间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,
,
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)求![]() 的面积;
的面积;
(3)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使
,使![]() 是等腰三角形.若不存在,请说明理由;若存在,请直接写出点
是等腰三角形.若不存在,请说明理由;若存在,请直接写出点![]() 的坐标
的坐标

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正比例函数y=![]() x与一次函数y=ax+7的图象相交于点P(4,n),过点A(2,0)作x轴的垂线,交一次函数的图象于点B,连接OB.
x与一次函数y=ax+7的图象相交于点P(4,n),过点A(2,0)作x轴的垂线,交一次函数的图象于点B,连接OB.
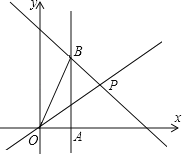
(1)求a值;
(2)求△OBP的面积;
(3)在坐标轴的正半轴上存在点Q,使△POQ是以OP为腰的等腰三角形,请直接写出Q点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com