
【题目】如图,正比例函数y=![]() x与一次函数y=ax+7的图象相交于点P(4,n),过点A(2,0)作x轴的垂线,交一次函数的图象于点B,连接OB.
x与一次函数y=ax+7的图象相交于点P(4,n),过点A(2,0)作x轴的垂线,交一次函数的图象于点B,连接OB.
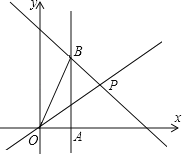
(1)求a值;
(2)求△OBP的面积;
(3)在坐标轴的正半轴上存在点Q,使△POQ是以OP为腰的等腰三角形,请直接写出Q点的坐标.
【答案】(1)a=-1;(2)7;(3)点Q的坐标为(5,0)或(8,0)或(0,5)或(0,6)
【解析】
(1)先由点P在正比例函数图象上求得n的值,再把点P坐标代入一次函数的解析式即可求出结果;
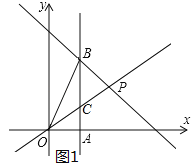
(2)易求点B坐标,设直线AB与OP交于点C,如图,则点C坐标可得,然后利用△OBP的面积=S△BCO+S△BCP代入相关数据计算即可求出结果;
(3)先根据勾股定理求出OP的长,再分两种情况:当OP=OQ时,以O为圆心,OP为半径作圆分别交y轴和x轴的正半轴于点Q1、Q2,如图2,则点Q1、Q2即为所求,然后利用等腰三角形的定义即可求出结果;当PO=PQ时,以P为圆心,OP为半径作圆分别交y轴和x轴的正半轴于点Q4、Q3,如图3,则点Q4、Q3也为所求,然后利用等腰三角形的性质即可求得结果.
解:(1)把点P(4,n)代入y=![]() x,得:n=
x,得:n=![]() ×4=3,∴P(4,3),
×4=3,∴P(4,3),
把P(4,3)代入y=ax+7得,3=4a+7,∴a=﹣1;
(2)∵A(2,0),AB⊥x轴,∴B点的横坐标为2,
∵点B在y=﹣x+7上,∴B(2,5),
设直线AB与OP交于点C,如图1,当x=2时,![]() ,∴C(2,
,∴C(2,![]() ),
),
∴△OBP的面积=S△BCO+S△BCP=![]() 2×(5﹣
2×(5﹣![]() )+
)+![]() (4﹣2)×(5﹣
(4﹣2)×(5﹣![]() )=7;
)=7;
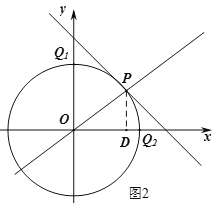
(3)过点P作PD⊥x轴于点D,∵P(4,3),∴OD=4,PD=3,∴![]() ,
,
当OP=OQ时,以O为圆心,OP为半径作圆分别交y轴和x轴的正半轴于点Q1、Q2,如图2,则点Q1、Q2即为所求,且Q2(5,0)、Q1(0,5);
当PO=PQ时,以P为圆心,OP为半径作圆分别交y轴和x轴的正半轴于点Q4、Q3,如图3,则点Q4、Q3也为所求,
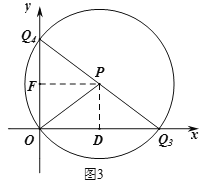
由于PO=PQ3,∴DQ3=DO=4,∴Q3(8,0),
过点P作PF⊥y轴于点F,同理可得:FQ4=FO=3,∴Q4(0,6).
综上所述,在坐标轴的正半轴上存在点Q,使△POQ是以OP为腰的等腰三角形,点Q的坐标为(5,0)或(8,0)或(0,5)或(0,6).


科目:初中数学 来源: 题型:
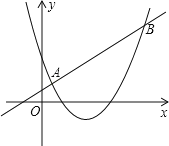
【题目】已知一次函数y1=kx+m和二次函数y2=ax2+bx+c的图象如图所示,它们的两个交点的横坐标是1和4,那么能够使得y1<y2的自变量x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠CAB=90°,∠CBA=50°,以AB为直径作⊙O交BC于点D,点E在边AC上,且满足ED=EA.
(1)求∠DOA的度数;
(2)求证:直线ED与⊙O相切.

查看答案和解析>>
科目:初中数学 来源: 题型:
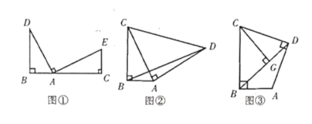
【题目】(l)观察猜想:如图①,点![]() 、
、![]() 、
、![]() 在同一条直线上,
在同一条直线上,![]() ,
,![]() 且
且![]() ,
,![]() ,则
,则![]() 和
和![]() 是否全等?__________(填是或否),线段
是否全等?__________(填是或否),线段![]() 之间的数量关系为__________
之间的数量关系为__________
(2)问题解决:如图②,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 为直角边向外作等腰
为直角边向外作等腰![]() ,连接
,连接![]() ,求
,求![]() 的长。
的长。
(3)拓展延伸:如图③,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 于点
于点![]() .求
.求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】齐齐哈尔市教育局想知道某校学生对扎龙自然保护区的了解程度,在该校随机抽取了部分学生进行问卷,问卷有以下四个选项:A.十分了解;B.了解较多:C.了解较少:D.不了解(要求:每名被调查的学生必选且只能选择一项).现将调查的结果绘制成两幅不完整的统计图.请根据两幅统计图中的信息回答下列问题:
(1)本次被抽取的学生共有_______名;
(2)请补全条形图;
(3)扇形图中的选项“C.了解较少”部分所占扇形的圆心角的大小为_______°;
(4)若该校共有![]() 名学生,请你根据上述调查结果估计该校对于扎龙自然保护区“十分了解”和“了解较多”的学生共有多少名?
名学生,请你根据上述调查结果估计该校对于扎龙自然保护区“十分了解”和“了解较多”的学生共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司引进![]() ,
,![]() 两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运
两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运![]() 小时,
小时,![]() 种机器人于某日
种机器人于某日![]() 时开始搬运,过了
时开始搬运,过了![]() 小时,
小时,![]() 种机器人也开始搬运,如图,线段
种机器人也开始搬运,如图,线段![]() 表示
表示![]() 种机器人的搬运量
种机器人的搬运量![]() (千克)与时间
(千克)与时间![]() (时)的函数图像,线段
(时)的函数图像,线段![]() 表示
表示![]() 种机器人的搬运量
种机器人的搬运量![]() (千克)与时间
(千克)与时间![]() (时)的函数图像,根据图像提供的信息,解答下列问题:
(时)的函数图像,根据图像提供的信息,解答下列问题:

(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)如果![]() 、
、![]() 两种机器人连续搬运
两种机器人连续搬运![]() 个小时,那么
个小时,那么![]() 种机器人比
种机器人比![]() 种机器人多搬运了多少千克?
种机器人多搬运了多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用小立方块搭一个几何体,使它从正面、上面看到的形状图如图所示,从上面看到的形状图的小正方形中的字母表示在该位置小立方块的个数.试回答下列问题:
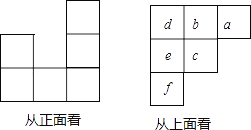
(1)a,b,c各表示几?
(2)这个几何体最少有几个小立方块搭成?最多呢?
(3)当d=e=1,f=2时,画出这个几何体从左面看到的形状图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com