练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，∠CAB＝90°，∠CBA＝50°，以AB为直径作⊙O交BC于点D，点E在边AC上，且满足ED＝EA．

    （1）求∠DOA的度数；

    （2）求证：直线ED与⊙O相切．

    【答案】（1）∠DOA =100°；（2）证明见解析.

    【解析】

    试题（1）根据∠CBA=50°，利用圆周角定理即可求得∠DOA的度数；（2）连接OE，利用SSS证明△EAO≌△EDO，根据全等三角形的性质可得∠EDO=∠EAO=90°，即可证明直线ED与⊙O相切．

    试题解析：（1）∵∠DBA=50°，∴∠DOA=2∠DBA=100°；

    （2）证明：连接OE，

    在△EAO和△EDO中，

    AO=DO，EA=ED，EO=EO，

    ∴△EAO≌△EDO，

    得到∠EDO=∠EAO=90°，

    ∴直线ED与⊙O相切．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知一个长方形的面积为6，它的一边为x，它的另一边长为y，周长为p．

    （1）填空：（用含x的代数式表示）

    ① y=__________；② p=__________；

    （2）当x值从2增大到a+2时，y的值减少了2，求增量a的值；

    （3）当x=m时，p的值为；当时，p的值为，求的值，并化成最简分式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＝AC＝10，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且∠CBF＝ ∠A，tan∠CBF＝ ， 则CF的长为

    （ ）

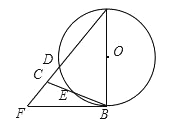    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，AB=AD，BC=DC，AC、BD相交于点O，点E在AO上，且OE=OC.

    （1）求证：∠1=∠2；

    （2）连结BE、DE，判断四边形BCDE的形状，并说明理由.

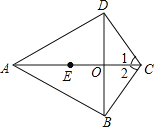
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一次函数y=2x+b.

    (1)它的图像与两坐标轴所围成的图形的面积等于4,求b的值;

    (2)它的图像经过一次函数y=-2x+1、y=x+4图像的交点,求b的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（材料阅读）我们曾解决过课本中的这样一道题目：

    如图，四边形是正方形，为边上一点，延长至，使，连接.……

    提炼1：绕点顺时针旋转90°得到；

    提炼2：；

    提炼3：旋转、平移、轴对称是图形全等变换的三种方式.

    （问题解决）（1）如图，四边形是正方形，为边上一点，连接，将沿折叠，点落在处，交于点，连接.可得： °；三者间的数量关系是 .

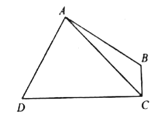
    （2）如图，四边形的面积为8，，，连接.求的长度.

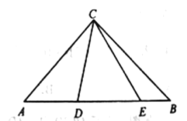
    （3）如图，在中，，，点在边上，.写出间的数量关系，并证明.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点D是△ABC内部的一点，BD=CD，过点D作DE⊥AB，DF⊥AC，垂足分别为E、F，且BE=CF．求证：AB=AC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正比例函数y＝x与一次函数y＝ax+7的图象相交于点P（4，n），过点A（2，0）作x轴的垂线，交一次函数的图象于点B，连接OB．

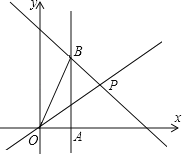
    （1）求a值；

    （2）求△OBP的面积；

    （3）在坐标轴的正半轴上存在点Q，使△POQ是以OP为腰的等腰三角形，请直接写出Q点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠ACD是△ABC的外角，∠ABC的平分线与∠ACD的平分线交于点A1，∠A1BC的平分线与∠A1CD的平分线交于点A2，…，∠An﹣1BC的平分线与∠An﹣1CD的平分线交于点An．设∠A＝θ．则：（1）∠A1＝_____；（2）∠A2＝_____；（3）∠An＝_____．

    查看答案和解析>>

    同步练习册答案