【题目】如图，在直角坐标系中，有菱形
，
点的坐标是
，双曲线
经过点
，且
，则
的值为（ ）
A. 40 B. 48 C. 64 D. 80
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
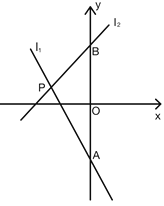
【题目】如图，已知直线
，直线
，
与
相交于点
，，分别与
轴相交于点
.
(1)求点P的坐标.
(2)若
，求x的取值范围.
(3)点
为x轴上的一个动点，过
作x轴的垂线分别交和于点
，当EF=3时，求m的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
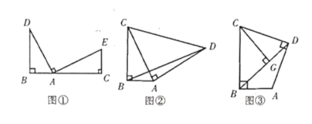
【题目】(l)观察猜想：如图①，点
、
、
在同一条直线上，
，
且
，
，则
和
是否全等？__________（填是或否），线段
之间的数量关系为__________
（2）问题解决：如图②，在
中，
，
，
，以
为直角边向外作等腰
，连接
，求的长。
（3）拓展延伸：如图③，在四边形
中，
,
,
,
，
于点
．求
的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某物流公司引进
，
两种机器人用来搬运某种货物，这两种机器人充满电后可以连续搬运
小时，种机器人于某日
时开始搬运，过了
小时，种机器人也开始搬运，如图，线段
表示种机器人的搬运量
（千克）与时间
（时）的函数图像，线段
表示种机器人的搬运量
（千克）与时间（时）的函数图像，根据图像提供的信息，解答下列问题：
（1）求关于的函数解析式；
（2）如果、两种机器人连续搬运个小时，那么种机器人比种机器人多搬运了多少千克？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，由6个长为2，宽为1的小矩形组成的大矩形网格，小矩形的顶点称为这个矩形网格的格点，由格点构成的几何图形称为格点图形（如：连接2个格点，得到一条格点线段；连接3个格点，得到一个格点三角形；…），请按要求作图（标出所画图形的顶点字母）．
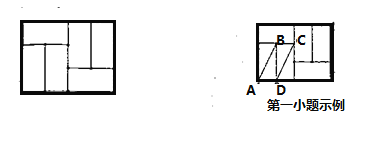
（1）画出4种不同于示例的平行格点线段；
（2）画出4种不同的成轴对称的格点三角形，并标出其对称轴所在线段；
（3）画出1个格点正方形，并简要证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场计划购进A，B两种新型节能台灯共100盏，A型灯每盏进价为30元，售价为45元；B型台灯每盏进价为50元，售价为70元．
（1）若商场预计进货款为3500元，求A型、B型节能灯各购进多少盏？
根据题意，先填写下表，再完成本问解答：
型号 | A型 | B型 |
购进数量（盏） | x | _____ |
购买费用（元） | _____ | _____ |
（2）若商场规定B型台灯的进货数量不超过A型台灯数量的3倍，应怎样进货才能使商场在销售完这批台灯时获利最多？此时利润为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数
的图象经过A（-1，0）、B（4，5）三点.
（1）求此二次函数的解析式；
（2）当x为何值时，y随x的增大而减小？
（3）当x为何值时，y＞0？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
