
【题目】某商场计划购进A,B两种新型节能台灯共100盏,A型灯每盏进价为30元,售价为45元;B型台灯每盏进价为50元,售价为70元.
(1)若商场预计进货款为3500元,求A型、B型节能灯各购进多少盏?
根据题意,先填写下表,再完成本问解答:
型号 | A型 | B型 |
购进数量(盏) | x | _____ |
购买费用(元) | _____ | _____ |
(2)若商场规定B型台灯的进货数量不超过A型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
【答案】(1)30x, y,50y;(2)商场购进A型台灯25盏,B型台灯75盏,销售完这批台灯时获利最多,此时利润为1875元.
【解析】
(1)设商场应购进A型台灯x盏,表示出B型台灯为y盏,然后根据“A,B两种新型节能台灯共100盏”、“进货款=A型台灯的进货款+B型台灯的进货款”列出方程组求解即可;
(2)设商场销售完这批台灯可获利y元,根据获利等于两种台灯的获利总和列式整理,再求出x的取值范围,然后根据一次函数的增减性求出获利的最大值.
(1)设商场应购进A型台灯x盏,则B型台灯为y盏,根据题意得:
![]()
解得:![]() .
.
答:应购进A型台灯75盏,B型台灯25盏.
故答案为:30x;y;50y;
(2)设商场应购进A型台灯x盏,销售完这批台灯可获利y元,则y=(45﹣30)x+(70﹣50)(100﹣x)=15x+2000﹣20x=﹣5x+2000,即y=﹣5x+2000.
∵B型台灯的进货数量不超过A型台灯数量的3倍,∴100﹣x≤3x,∴x≥25.
∵k=﹣5<0,y随x的增大而减小,∴x=25时,y取得最大值,为﹣5×25+2000=1875(元).
答:商场购进A型台灯25盏,B型台灯75盏,销售完这批台灯时获利最多,此时利润为1875元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(材料阅读)我们曾解决过课本中的这样一道题目:
如图,四边形![]() 是正方形,
是正方形,![]() 为
为![]() 边上一点,延长
边上一点,延长![]() 至
至![]() ,使
,使![]() ,连接
,连接![]() .……
.……
提炼1:![]() 绕点
绕点![]() 顺时针旋转90°得到
顺时针旋转90°得到![]() ;
;
提炼2:![]() ;
;
提炼3:旋转、平移、轴对称是图形全等变换的三种方式.
![]()
(问题解决)(1)如图,四边形![]() 是正方形,
是正方形,![]() 为
为![]() 边上一点,连接
边上一点,连接![]() ,将
,将![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在
落在![]() 处,
处,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .可得:
.可得:![]() °;
°;![]() 三者间的数量关系是
三者间的数量关系是

(2)如图,四边形![]() 的面积为8,
的面积为8,![]() ,
,![]() ,连接
,连接![]() .求
.求![]() 的长度.
的长度.
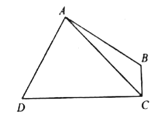
(3)如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() .写出
.写出![]() 间的数量关系,并证明.
间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
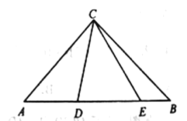
【题目】如图,等腰三角形ABC底边BC的长为4 cm,面积为12 cm2,腰AB的垂直平分线EF交AB于点E,交AC于点F,若D为BC边上的中点,M为线段EF上一点,则△BDM的周长最小值为( )
A. 5 cm B. 6 cm C. 8 cm D. 10 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
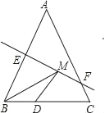
【题目】如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…,∠An﹣1BC的平分线与∠An﹣1CD的平分线交于点An.设∠A=θ.则:(1)∠A1=_____;(2)∠A2=_____;(3)∠An=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小董设计的“作已知圆的内接正三角形”的尺规作图过程.
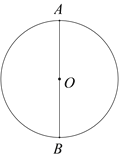
已知:⊙O.
求作:⊙O的内接正三角形.
作法:如图,
①作直径AB;
②以B为圆心,OB为半径作弧,与⊙O交于C,D两点;
③连接AC,AD,CD.
所以△ACD就是所求的三角形.
根据小董设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:在⊙O中,连接OC,OD,BC,BD,
∵OC=OB=BC,
∴△OBC为等边三角形(_______________)(填推理的依据).
∴∠BOC=60°.
∴∠AOC=180°-∠BOC=120°.
同理∠AOD=120°,
∴∠COD=∠AOC=∠AOD=120°.
∴AC=CD=AD(_______________)(填推理的依据).
∴△ACD是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
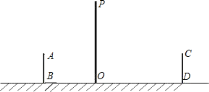
【题目】如图,是小亮晚上在广场散步的示意图,图中线段![]() 表示站立在广场上的小亮,线段
表示站立在广场上的小亮,线段![]() 表示直立在广场上的灯杆,点
表示直立在广场上的灯杆,点![]() 表示照明灯的位置.
表示照明灯的位置.
![]() 在小亮由
在小亮由![]() 处沿
处沿![]() 所在的方向行走到达
所在的方向行走到达![]() 处的过程中,他在地面上的影子长度越来越________(用“长”或“短”填空);请你在图中画出小亮站在
处的过程中,他在地面上的影子长度越来越________(用“长”或“短”填空);请你在图中画出小亮站在![]() 处的影子
处的影子![]() ;
;
![]() 当小亮离开灯杆的距离
当小亮离开灯杆的距离![]() 时,身高为
时,身高为![]() 的小亮的影长为
的小亮的影长为![]() ,
,
①灯杆的高度为多少![]() ?
?
②当小亮离开灯杆的距离![]() 时,小亮的影长变为多少
时,小亮的影长变为多少![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某开发公司生产的 960 件新产品需要精加工后,才能投放市场,现甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用 20 天,而甲工厂每天加工的数量是乙工厂每天加工的数量的![]() ,公司需付甲工厂加工费用为每天 80 元,乙工厂加工费用为每天 120 元.
,公司需付甲工厂加工费用为每天 80 元,乙工厂加工费用为每天 120 元.
(1)甲、乙两个工厂每天各能加工多少件新产品?
(2)公司制定产品加工方案如下:可以由每个厂家单独完成,也可以由两个厂家合作完成.在加工过程中,公司派一名工程师每天到厂进行技术指导,并负担每天 15 元的午餐补助费, 请你帮公司选择一种既省时又省钱的加工方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com