
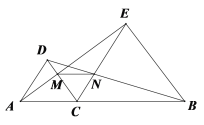
【题目】如图,点C在AB上,![]() 、
、![]() 均是等边三角形,
均是等边三角形,![]() 、
、![]() 分别与
分别与![]() 交于点
交于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() 为等边三角形;④
为等边三角形;④![]() ∥
∥![]() ;⑤DC=DN正确的有( )个
;⑤DC=DN正确的有( )个
A.2个B.3个C.4个D.5
【答案】C
【解析】
首先根据等边三角形的性质,运用SAS证明△ACE≌△DCB,即可得出AE=DB;再由ASA判定△AMC≌△DNC,得出CM=CN;由∠MCN=60°得出△CMN为等边三角形;再由内错角相等两直线平行得出MN∥BC;最后由∠DCN=∠CNM=60°,得出DC≠DN,即可判定.
∵![]() 、
、![]() 均是等边三角形,
均是等边三角形,
∴∠DCA=∠ECB=60°,AC=DC,EC=BC
∴∠DCE=60°
∴∠DCA+∠DCE=∠ECB+∠DCE,即∠ACE=∠DCB
∴△ACE≌△DCB(SAS)
∴AE=DB,故①正确;
∵△ACE≌△DCB,
∴∠MAC=∠NDC,
∵∠ACD=∠BCE=60°,
∴∠MCA=∠DCN=60°,
在△AMC和△DNC中
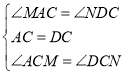
∴△AMC≌△DNC(ASA),
∴CM=CN,故②正确;
∴△CMN为等边三角形,故③正确;
∴∠NMC=∠NCB=60°,
∴MN∥BC.故④正确;
∵∠DCN=∠CNM=60°
∴DC≠DN,故⑤错误;
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,![]() ,AE交BC于点P,交DC的延长线于点E,点P为AE的中点.
,AE交BC于点P,交DC的延长线于点E,点P为AE的中点.
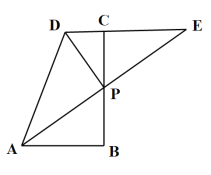
(1)求证:点P也是BC的中点.
(2)若![]() ,且
,且![]() ,求AP的长.
,求AP的长.
(3)在(2)的条件下,若线段AE上有一点Q,使得![]() 是等腰三角形,求
是等腰三角形,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
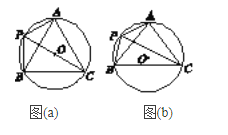
【题目】如图所示,在平面直角坐标系中,△ABC是⊙O的内接三角形,AB=AC,点P是![]() 的中点,连结PA,PB,PC.
的中点,连结PA,PB,PC.
(1)如图(a),若∠BPC=60°,求证:AC=![]() AP;
AP;
(2)如图(b),若sin∠BPC=![]() ,求tan∠PAB的值.
,求tan∠PAB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
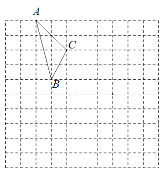
【题目】如图,在平面直角坐标系中,已知△ ABC 的三个顶点的坐标分别为 A(-3,5),B(-2,1).
(1)请在如图所示的网格内画出平面直角坐标系,并写出 C 点坐标;
(2)先将△ABC 沿 x 轴翻折,再沿 x 轴向右平移 4 个单位长度后得到△A1B1C1,请 在网格内画出△A1B1C1;
(3)在(2)的条件下,△ABC 的边 AC 上一点 M(a,b)的对应点 M1 的坐标是 .(友情提醒:画图结果确定后请用黑色签字笔加黑)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你用学习 “一次函数”时积累的经验和方法研究函数 y=![]() 的图像和性质,并 解决问题.
的图像和性质,并 解决问题.
(1)按照下列步骤,画出函数 y=![]() 的图像;
的图像;
①列表;

②描点;
③连线.

(友情提醒:画图结果确定后请用黑色签字笔加黑)
(2)观察图像,填空;
①当 x 时,y 随 x 的增大而减小; 当 x 时,y 随 x 的增大而增大;
②此函数有最 值(填“大”或“小”),其值是 ;
(3)根据图像,不等式![]() >
> ![]() x
x ![]() 的解集为 .
的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=90°.
(1)尺规作图:按下列要求完成作图(保留作图痕迹,请标明字母)
①作线段AC的垂直平分线l,交AC于点O;
②连接BO并延长,在BO的延长线上截取OD,使得OD=OB;
③连接DA、DC.
(2)判断四边形ABCD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个长方形的面积为6,它的一边为x,它的另一边长为y,周长为p.
(1)填空:(用含x的代数式表示)
① y=__________;② p=__________;
(2)当x值从2增大到a+2时,y的值减少了2,求增量a的值;
(3)当x=m时,p的值为![]() ;当
;当![]() 时,p的值为
时,p的值为![]() ,求
,求![]() 的值,并化成最简分式.
的值,并化成最简分式.
查看答案和解析>>
科目:初中数学 来源: 题型:
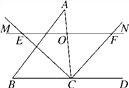
【题目】如图,在△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)探究线段OE与OF的数量关系并加以证明;
(2)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?并说明理由;
(3)当点O在边AC上运动时,四边形BCFE可能是菱形吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
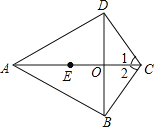
【题目】如图,在四边形ABCD中,AB=AD,BC=DC,AC、BD相交于点O,点E在AO上,且OE=OC.
(1)求证:∠1=∠2;
(2)连结BE、DE,判断四边形BCDE的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com